【题目】如图,D为等边三角形ABC内的一点, DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ABCD′=6+![]() ,其中正确的有( )
,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
参考答案:
【答案】B
【解析】
连结DD′,根据旋转的性质得AD=AD′,∠DAD′=60°,可判断△ADD′为等边三角形,则DD′=5,即可对①进行判断;由△ABC为等边三角形得到AB=AC,∠BAC=60°,
则把△ABD逆时针旋转60°后,AB与AC重合,AD与AD′重合,于是可对③进行判断;再根据勾股定理的逆定理得到△DD′C为直角三角形,则可对②④进行判断;由于S四边形ADCD′=S△ADD′+S△D′DC,利用等边三角形的面积公式和直角三角形面积公式计算后可对⑤进行判断.
连结DD′,如图,
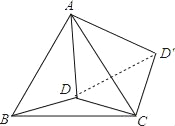
∵线段AD以点A为旋转中心逆时针旋转60°得到线段AD′,
∴AD=AD′,∠DAD′=60°,
∴△ADD′为等边三角形,
∴DD′=5,所以①正确;
∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∴把△ABD逆时针旋转60°后,AB与AC重合,AD与AD′重合,
∴△ACD′可以由△ABD绕点A逆时针旋转60°得到,所以③正确;
∴D′C=DB=4,
∵DC=3,
在△DD′C中,
∵32+42=52,
∴DC2+D′C2=DD′2,
∴△DD′C为直角三角形,
∴∠DCD′=90°,
∵△ADD′为等边三角形,
∴∠ADD′=60°,
∴∠ADC≠150°,所以②错误;
∵∠DCD′=90°,
∴DC⊥CD′,
∴点D到CD′的距离为3,所以④正确;
∵S△ADD′+S△D′DC=![]() ×52+
×52+![]() ×3×4=6+
×3×4=6+![]() ,
,
所以⑤错误.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BC于F,交B0于H,连接OG,CC.
(1)求证:AH=BE;
(2)试探究:∠AGO的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=
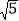 ,求△OGC的面积.
,求△OGC的面积.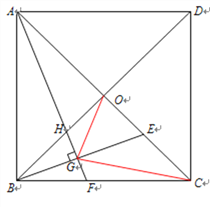
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A.
 B.
B.  C.
C. 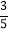 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量
单价(元/m3)
不超出80m3的部分
2.5
超出80m3不超出130m3的部分
a
超出130m3的部分
a+0.5
(1)若甲用户3月份用气125m3,缴费335元,求a的值;
(2)在(1)的条件下,若乙用户3月份缴费392元,则乙用户3月份的用气量是多少?
-
科目: 来源: 题型:
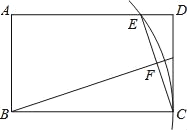
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
A.
 B.
B. 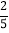 C.
C. 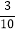 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场欲购进果汁饮料和碳酸饮料共60箱,两种饮料每箱的进价和售价如下表所示。设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注:总利润=总售价-总进价)。
(1)设商场购进碳酸饮料y箱,直接写出y与x的函数解析式;
(2)求总利润w关于x的函数解析式;
(3)如果购进两种饮料的总费用不超过2100元,那么该商场如何进货才能获利最多?并求出最大利润。
饮料
果汁饮料
碳酸饮料
进价(元/箱)
40
25
售价(元/箱)
52
32
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:我们知道:如果点A.B在数轴上分别表示有理数a、b,那么A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|ab|.
根据上述材料,利用数轴解答下列问题:

(1)如果点A在数轴上表示2,将点A先向左平移2个单位长度,再向右移动7个单位长度,那么终点B在数轴上表示的数是___;
(2)数轴上表示x和1的两个点之间的距离是___;
(3)若|x3|+|x+2|=7,则x的值是___;
(4)在(1)的条件下,设点P在数轴上表示的数为x,当|PA||PB|=2时,则x的值是___.
相关试题

