【题目】△ ![]() 中,
中, ![]() .取
.取 ![]() 边的中点
边的中点 ![]() ,作
,作 ![]() ⊥
⊥ ![]() 于点
于点 ![]() ,取
,取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,
, ![]() 交于点
交于点 ![]() .
.
(1)如图1,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并求
并求 ![]() 的值;
的值;
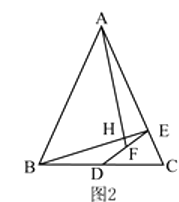
(2)如图2,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并用含
并用含 ![]() 的式子表示
的式子表示 ![]() .
.
参考答案:
【答案】
(1)解:如图1,连接AD,
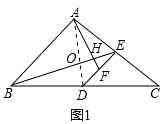
∵AB=AC,点D是BC的中点,
∴∠ABC=∠C,∠BAD=∠DAC= ![]() ∠BAC,AD⊥BC,
∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,∴ ![]() ,即ADCE=BDDE.
,即ADCE=BDDE.
∵点D是BC的中点,点F是DE的中点,
∴BD= ![]() BC,DE=2DF,
BC,DE=2DF,
∴ADCE═ ![]() BC2DF=BCDF,
BC2DF=BCDF,
∴ ![]() ,
,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴ ![]() ,在Rt△ADB中,
,在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°- ![]() ∠BAC,BD=
∠BAC,BD= ![]() BC,
BC,
∴tan∠ABD=tan(90°- ![]() ∠BAC)=
∠BAC)= ![]() ,
,
∴ ![]() =
= ![]() tan(90°-
tan(90°- ![]() ∠BAC).
∠BAC).
∵△AFD∽△BEC,
∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°
根据以上结论可得:∠AHB=90°, ![]() =
= ![]() tan(90°-
tan(90°- ![]() ×90°)=
×90°)= ![]() ;∴AF⊥BE,
;∴AF⊥BE, ![]() =
= ![]()
(2)解:如图2,
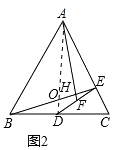
根据以上结论可得:∠AHB=90°, ![]() =
= ![]() tan(90°-
tan(90°- ![]() α);∴AF⊥BE, =
α);∴AF⊥BE, = ![]() tan(90°-
tan(90°- ![]() α)
α)
【解析】(1)由AB=AC,点D是BC的中点,根据三线合一,得到AD⊥BC,由DE⊥AC,根据同角的余角相等,得到∠ADE=∠C;得到△ADB∽△DEC,得到比例,即ADCE=BDDE;由已知得到ADCE=BCDF,又∠ADE=∠C,得到△AFD∽△BEC,得到比例,在Rt△ADB中,根据三角函数定义,得到∠DAF=∠CBE,由三角形内角和定理求出∠AHO=90°,即∠AHB=90°,根据以上结论可得![]()
【考点精析】掌握相似三角形的判定与性质和锐角三角函数的定义是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).
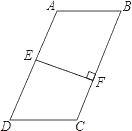
-
科目: 来源: 题型:
查看答案和解析>>【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度
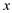 /℃
/℃……
-4
-2
0
2
4
4.5
……
植物每天高度增长量
 /mm
/mm……
41
49
49
41
25
19.75
……
这些数据说明:植物每天高度增长量
 关于温度
关于温度 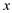 的函数是反比例函数、一次函数和二次函数中的一种.
的函数是反比例函数、一次函数和二次函数中的一种.
(1)你认为是哪一种函数,并求出它的函数关系式;
(2)温度为多少时,这种植物每天高度增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度x应该在哪个范围内选择?请直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的方格纸中,每一个小正方形的边长都为1.
(1)∠BCD是不是直角?请说明理由;
(2)求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答会告诉你方法.
(1)阅读下列材料:
问题:利用一元一次方程将
 化成分数.
化成分数.解:设
 .
.方程两边都乘以10,可得
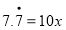 .
.由
 和
和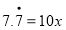 ,可得
,可得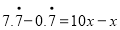 即
即 .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)解得
 ,即
,即 .
.填空:将0.
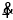 写成分数形式为 .
写成分数形式为 .(2)请你仿照上述方法把小数1.
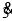 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程. -
科目: 来源: 题型:
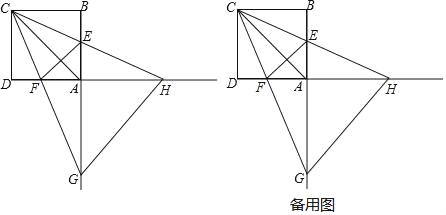
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
相关试题

