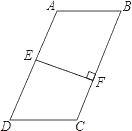
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).
参考答案:
【答案】(1)15;(2)=.
【解析】试题分析:(1)∵AB=DC,AB∥DC,
∴四边形ABCD是平行四边形,
∴四边形ABCD的面积S=5×3=15,
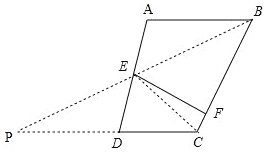
(2)如图,连接EC,延长CD、BE交于点P,
∵E是AD中点,
∴AE=DE,
又∵AB∥CD,
∴∠ABE=∠P,∠A=∠PDE,
在△ABE和△DPE中,
∵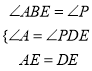 ,
,
∴△ABE≌△DPE(AAS),
∴S△ABE=S△DPE,BE=PE,
∴S△BCE=S△PCE,
则S四边形ABCD=S△ABE+S△CDE+S△BCE
=S△PDE+S△CDE+S△BCE
=S△PCE+S△BCE
=2S△BCE
=2×![]() ×BC×EF
×BC×EF
=15,
∴当AB>DC,则此时四边形ABCD的面积S′=S,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.
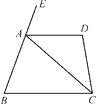
(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
-
科目: 来源: 题型:
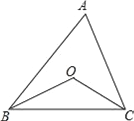
查看答案和解析>>【题目】如图,已知点O是△ABC的两条角平分线的交点,
(1)若∠A=30°,则∠BOC的大小是 ;
(2)若∠A=60°,则∠BOC的大小是 ;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
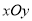 中,抛物线
中,抛物线 过点
过点 ,
, ,与
,与 轴交于点
轴交于点 .
.(1)求抛物线
 的函数表达式;
的函数表达式;(2)若点
 在抛物线
在抛物线 的对称轴上,当
的对称轴上,当 的周长最小时,求点
的周长最小时,求点 的坐标;
的坐标;(3)在抛物线
 的对称轴上是否存在点
的对称轴上是否存在点 ,使
,使 成为以
成为以 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB的中点,点D在线段CB上.

(1)图中共有 条线段.
(2)图中AD=AC+CD,BC=AB﹣AC,类似地,请你再写出两个有关线段的和与差的关系式:
① ;② .
(3)若AB=8,DB=1.5,求线段CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程3x2+27=0,得该方程的根是( )
A. x=±3 B. x=3 C. x=﹣3 D. 无实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长分别是2cm、5cm,则它的周长为cm.
相关试题

