【题目】有这样一道习题:如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.
(1)证明:RP=RQ;
(2)请探究下列变化:
A、变化一:交换题设与结论.已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.证明:RQ为⊙O的切线.

B、变化二:运动探求. ①如图2,若OA向上平移,变化一中结论还成立吗?(只交待判断) 答:_________.
②如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,原题中的结论还成立吗?为什么?
参考答案:
【答案】(1)证明见解析;
(2)变化一:证明见解析;变化二:①结论成立;②结论成立,理由见解析.
【解析】试题分析:(1)首先连接OQ,由切线的性质,可得∠OQB+∠BQR=90°,又由OA⊥OB,可得∠OPB+∠B=90°,继而可证得∠PQR=∠BPO=∠RPQ,则可证得RP=RQ,
(2)A、变化一,连接OQ, 证明∠OQR=90°即可;
B、变化二:①若OA向上平移,变化一中的结论还成立,证明思路同变化一;
②如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,原题中的结论还成立,连接OQ,证明思路同(1);
试题解析:(1)连接OQ,
∵OQ=OB,∴∠OBP=∠OQP,
又∵QR为⊙O的切线,
∴OQ⊥QR,
即∠OQP+∠PQR=90°,
而∠OBP+∠OPB=90°,
故∠PQR=∠OPB,
又∵∠OPB与∠QPR为对顶角,
∴∠OPB=∠QPR,∴∠PQR=∠QPR
∴RP=RQ;
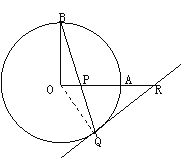
变化一、连接OQ,
∵RP=RQ,
∴∠PQR=∠QPR=∠BPO,
又∵OB=OQ,OA⊥OB,
∴∠OQB=∠OBQ,∠OBQ+∠BPO=90°,
∴∠OQB+∠PQR=90°,
即∠OQR=90°,
∴RQ为⊙O的切线;

变化二、(1)结论成立 ,
连接OQ,
∵RP=RQ,
∴∠PQR=∠QPR=∠BPM,
又∵OB=OQ,RP⊥OB,
∴∠OQB=∠OBQ,∠OBQ+∠BPM=90°,
∴∠OQB+∠PQR=90°,
即∠OQR=90°,
∴RQ为⊙O的切线;
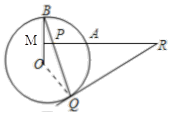
(2)结论成立,

连接OQ,
∵RQ是⊙O的切线,
∴OQ⊥QR,
∴∠OQB+∠PQR=90°,
∵OA⊥OB,
∴∠OPB+∠B=90°,
又∵OB=OQ,
∴∠OQB=∠B,
∴∠PQR=∠BPO=∠RPQ,
∴RP=RQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润
 与投资量
与投资量 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润 与投资量
与投资量 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
(1)分别求出利润
 与
与 关于投资量
关于投资量 的函数关系式;
的函数关系式;(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场试销一种成本价为每件60元的服装,规定试销期间销售单价不低于成本单价,获利不得高于40%.经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=80时,y=40;x=70时,y=50.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程a2x2+(2a-1)x+1=0有两个不相等的实数根x1,x2.(1)求a的取值范围;(2)是否存在实数a,使方程的两个实数根互为相反数?如果存在,求出a的值;如果不存在,说明理由.
解:(1)根据题意,得△=(2a-1)2-4a2>0,解得a<
 .
.∴当a<0时,方程有两个不相等的实数根.
(2)存在,如果方程的两个实数根x1,x2互为相反数,则x1+x2=-
 =0 ①,
=0 ①,解得a=
 ,经检验,a=
,经检验,a= 是方程①的根.
是方程①的根.∴当a=
 时,方程的两个实数根x1与x2互为相反数.
时,方程的两个实数根x1与x2互为相反数.上述解答过程是否有错误?如果有,请指出错误之处,并解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA.

(1)求△OAB的面积;
(2)若抛物线y=-x2-2x+c经过点A.
①求c的值;
②将抛物线向下平移m个单位长度,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加某网店的“翻牌抽奖”活动.如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.

(1)如果随机翻1张牌,求抽中20元奖品的概率;
(2)如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,求所获奖品总值不低于30元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,根据图中信息解答下列问题:
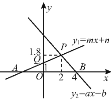
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
相关试题

