【题目】一家电信公司推出两种移动电话计费方法:计费方法![]() 是每月收月租费
是每月收月租费![]() 元,通话时间不超过
元,通话时间不超过![]() 分钟的部分免费,超过
分钟的部分免费,超过![]() 分的按每分钟
分的按每分钟![]() 元加收通话费;计费方法
元加收通话费;计费方法![]() 是每月收月租费
是每月收月租费![]() 元,通话时间不超过
元,通话时间不超过![]() 分钟的部分免费,超过
分钟的部分免费,超过![]() 分的按每分钟
分的按每分钟![]() 元加收通话费.设通话时间为
元加收通话费.设通话时间为![]() 分.
分.
(![]() )用代数式表示通话
)用代数式表示通话![]() 分钟的通话费用.
分钟的通话费用.
(![]() )用计费方法
)用计费方法![]() 的用户一个月累计通话
的用户一个月累计通话![]() 分钟所需的话费,若改用计费方法
分钟所需的话费,若改用计费方法![]() ,则可多通话多少分钟?
,则可多通话多少分钟?
(![]() )按
)按![]() ,
, ![]() 两种计费方法,所需的话费会相等吗?如果会,请指出相等的时间.
两种计费方法,所需的话费会相等吗?如果会,请指出相等的时间.
参考答案:
【答案】见解析.
【解析】试题分析:(1)根据计费方法![]() 表示出通话费用即可;
表示出通话费用即可;
(2)根据题意列出方程,求出方程的解即可得到结果;
(3)当![]() 时,按照方法
时,按照方法![]() 计费需
计费需![]() 元,按方法
元,按方法![]() 计费需
计费需![]() 元.
元.
根据题意列出方程,求出方程的解即可得到结果.
试题解析:(![]() )①计费方法
)①计费方法![]() :当
:当![]() 时,通话费用
时,通话费用![]() 元,当
元,当![]() 时,通话费用为
时,通话费用为![]() .
.
②计费方法![]() ,当
,当![]() 时,费用为
时,费用为![]() 元.
元.
当![]() 时,费用为
时,费用为![]() .
.
(![]() )若为方法
)若为方法![]() 计费,所需费用为
计费,所需费用为![]() 元,若改为方法
元,若改为方法![]() 计算,
计算,
![]() 元可通话分钟为
元可通话分钟为![]() 分钟,
分钟,
则可多通话时间为![]() 分钟.
分钟.
(![]() )会相等.
)会相等.
当![]() 时,按照方法
时,按照方法![]() 计费需
计费需![]() 元,按方法
元,按方法![]() 计费需
计费需![]() 元.
元.
当![]() 时,可得
时,可得![]() ,
,
所以当通话时间为![]() 分钟时,两种计费方法所需话费相等.
分钟时,两种计费方法所需话费相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,∠B=25°,AB=5,则BC的长为( )
A.5sin25°B.5tan65°C.5cos25°D.5tan25°
-
科目: 来源: 题型:
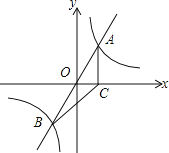
查看答案和解析>>【题目】如图,直线y=mx与双曲线y=
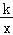 相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.(1)求反比例函数的表达式;
(2)根据图象直接写出当mx>
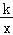 时,x的取值范围;
时,x的取值范围;(3)在平面内是否存在一点D,使四边形ABDC为平行四边形?若存在,请求出点D坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
-
科目: 来源: 题型:
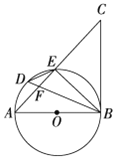
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D是弧AE上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DF·DB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点
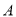 、
、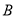 对应的数分别为
对应的数分别为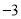 、
、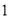 ,点
,点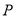 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为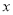 .
.(
 )若点
)若点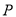 到点
到点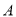 ,点
,点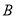 的距离相等,求点
的距离相等,求点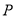 对应的数.
对应的数.(
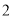 )数轴上是否存在点
)数轴上是否存在点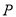 ,使点
,使点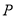 到点
到点 、点
、点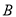 的距离之和为
的距离之和为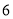 ?若存在,请求出
?若存在,请求出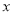 的值;若不存在,说明理由.
的值;若不存在,说明理由.(
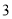 )点
)点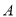 、点
、点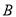 分别以
分别以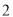 个单位长度/分、
个单位长度/分、 个单位长度/分的速度向右运动,同时点
个单位长度/分的速度向右运动,同时点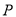 以
以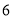 个单位长度/分的速度从
个单位长度/分的速度从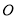 点向左运动.当遇到
点向左运动.当遇到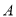 时,点
时,点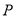 立即以同样的速度向右运动,并不停地往返于点
立即以同样的速度向右运动,并不停地往返于点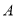 与点
与点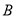 之间,求当点
之间,求当点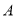 与点
与点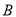 重合时,点
重合时,点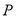 所经过的总路程是多少?
所经过的总路程是多少? -
科目: 来源: 题型:
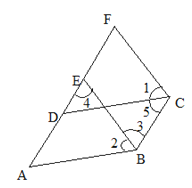
查看答案和解析>>【题目】如图,已知
 ,
,  ,
, 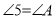 ,试说明:BE∥CF.
,试说明:BE∥CF.完善下面的解答过程,并填写理由或数学式:
解:∵
 (已知)
(已知)∴AE∥ ( )
∴
 ( )
( )∵
 (已知)
(已知)∴
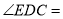 ( )
( )∴DC∥AB( )
∴
 ( )
( )即

∵
 (已知)
(已知)∴
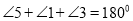 ( )
( )即

∴BE∥CF( ) .
相关试题

