【题目】如图,在平面直角坐标系中,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA= ![]() ,反比例函数y=
,反比例函数y= ![]() (k>0)的图像过CD的中点E.
(k>0)的图像过CD的中点E.
(1)求k的值;
(2)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图像上,并说明理由.
参考答案:
【答案】
(1)
解:在Rt△ACD中,CD=2,AD= ![]() ,
,
∴AC= ![]() =1,
=1,
∴OC=OA+AC=2+1=3,
∴D点坐标为(3,2),
∵点E为CD的中点,
∴点E的坐标为(3,1),
∴k=3×1=3
(2)
解:点G在反比例函数的图像上.理由如下:
∵△BFG和△DCA关于某点成中心对称,
∴△BFG≌△DCA,
∴FG=CA=1,BF=DC=2,∠BFG=∠DCA=90°,
而OB=AC=1,
∴OF=OB+BF=1+2=3,
∴G点坐标为(1,3),
∵1×3=3,
∴G(1,3)在反比例函数y= ![]() 的图像上
的图像上
【解析】(1)先利用勾股定理计算出AC=1,再确定C点坐标,然后根据点E为CD的中点可得到点E的坐标为(3,1),则可根据反比例函数图像上点的坐标特征求得k=3;(2)根据中心对称的性质得△BFG≌△DCA,所以FG=CA=1,BF=DC=2,∠BFG=∠DCA=90°,则可得到G点坐标为(1,3),然后根据反比例函数图像上点的坐标特征判断G点是否在函数y= ![]() 的图像上.
的图像上.
【考点精析】认真审题,首先需要了解反比例函数的性质(性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大).
-
科目: 来源: 题型:
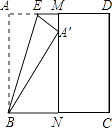
查看答案和解析>>【题目】如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.

(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接河南省第30届青少年科技创新大赛,某中学向七年级学生征集科幻画作品,李老师从七年级12个班中随机抽取了A、B、C、D四个班,对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图(如图)

(1)李老师所调查的4个班征集到作品共件,其中B班征集到作品 , 请把图补充完整;
(2)李老师所调查的四个班平均每个班征集到作品多少件?请估计全年级共征集到作品多少件?
(3)如果全年级参展作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生.现在要抽两人去参加学校总结表彰座谈会,用树状图或列表法求出恰好抽中一男一女的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】小华和小丽两人玩数字游戏,先由小丽心中任意想一个数字记为x,再由小华猜小丽刚才想的数字,把小华猜的数字记为y,且他们想和猜的数字只能在1,2,3,4这四个数中.
(1)请用树状图或列表法表示了他们想和猜的所有情况;
(2)如果他们想和猜的数相同,则称他们“心灵相通”.求他们“心灵相通”的概率;
(3)如果他们想和猜的数字满足|x﹣y|≤1,则称他们“心有灵犀”.求他们“心有灵犀”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB≠BC,连接AC,AE是∠BAD的平分线,交边DC的延长线于点F.

(1)证明:CE=CF;
(2)若∠B=60°,BC=2AB,试判断四边形ABFC的形状,并说明理由.(如图2所示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣
 x﹣2(a≠0)的图像与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
x﹣2(a≠0)的图像与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.
相关试题

