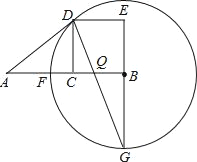
【题目】设C为线段AB的中点,四边形BCDE是以BC为一边的正方形.以B为圆心,BD长为半径的⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
求证:(1)AD是⊙B的切线;(2)AD=AQ;(3)BC2=CFEG.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)连接BD,由DC⊥AB,C为AB的中点,由线段垂直平分线的性质,可得AD=BD,再根据正方形的性质,可得∠ADB=90°;
(2)由BD=BG与CD∥BE,利用等边对等角与平行线的性质,即可求得∠G=∠CDG=∠BDG=![]() ∠BCD=22.5°,继而求得∠ADQ=∠AQD=67.5°,由等角对等边,可证得AD=AQ;
∠BCD=22.5°,继而求得∠ADQ=∠AQD=67.5°,由等角对等边,可证得AD=AQ;
(3)易求得∠GDE=∠GDB+∠BDE=67.5°=∠DFE,∠DCF=∠E=90°,即可证得Rt△DCF∽Rt△GED,根据相似三角形的对应边成比例,即可证得结论.
试题解析:
(1)连接BD,
∵四边形BCDE是正方形,
∴∠DBA=45°,∠DCB=90°,即DC⊥AB,
∵C为AB的中点,
∴CD是线段AB的垂直平分线,
∴AD=BD,
∴∠DAB=∠DBA=45°,
∴∠ADB=90°,
即BD⊥AD,
∵BD为半径,
∴AD是⊙B的切线;
(2)∵BD=BG,
∴∠BDG=∠G,
∵CD∥BE,
∴∠CDG=∠G,
∴∠G=∠CDG=∠BDG=![]() ∠BCD=22.5°,
∠BCD=22.5°,
∴∠ADQ=90°﹣∠BDG=67.5°,∠AQB=∠BQG=90°﹣∠G=67.5°,
∴∠ADQ=∠AQD,
∴AD=AQ;
(3)连接DF,
在△BDF中,BD=BF,
∴∠BFD=∠BDF,
又∵∠DBF=45°,
∴∠BFD=∠BDF=67.5°,
∵∠GDB=22.5°,
在Rt△DEF与Rt△GCD中,
∵∠GDE=∠GDB+∠BDE=67.5°=∠DFE,∠DCF=∠E=90°,
∴Rt△DCF∽Rt△GED,
∴![]() ,
,
又∵CD=DE=BC,
∴BC2=CFEG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 a b , a 与b 两个数在数轴上对应的点分别为点 A 、点 B ,求 A 、 B 两点之间的距离.
(探索)
小明利用绝对值的概念,结合数轴,进行探索:
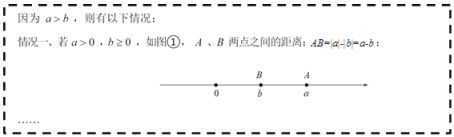
(1)补全小明的探索
(应用)
(2)若点C 对应的数c ,数轴上点C 到A、B 两点的距离相等,求c .(用含a、b 的代数式表示)
(3)若点 D对应的数 d ,数轴上点 D 到 A 的距离是点 D 到 B 的距离的nn 0 倍,请探索 n 的取值范围与点 D 个数的关系,并直接写出a、b 、d、n 的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的A、B两点所表示的数分别为a、b,a+b<0,ab<0.

(1)原点O的位置在
A.点A的右边
B.点B的左边
C.点A与点B之间 ,且靠近点A
D.点A与点B之间 ,且靠近点B
(2)若a-b=2,
①利用数轴比较大小,a 1,b -1;(填“>”、“<”或“=”).
②化简:|a-1|+|b+1|.
-
科目: 来源: 题型:
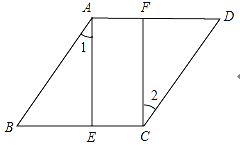
查看答案和解析>>【题目】如图,点E,F在菱形ABCD的对边上,AE⊥BC.∠1=∠2.
(1)判断四边形AECF的形状,并证明你的结论.
(2)若AE=4,AF=2,试求菱形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 两地相距300
两地相距300 ,甲、乙两车同时从
,甲、乙两车同时从 地出发驶向
地出发驶向 地,甲车到达
地,甲车到达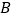 地后立即返回,如图是两车离
地后立即返回,如图是两车离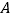 地的距离
地的距离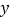 (
(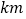 )与行驶时间
)与行驶时间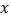 (
(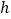 )之间的函数图象.
)之间的函数图象.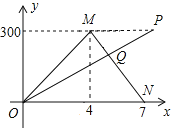
(1)求甲车行驶过程中
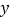 与
与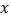 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量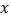 的取值范围.
的取值范围.(2)若两车行驶5
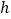 相遇,求乙车的速度.
相遇,求乙车的速度. -
科目: 来源: 题型:
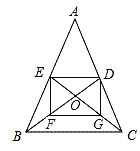
查看答案和解析>>【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为_____.

相关试题

