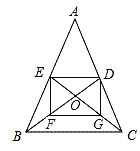
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.
参考答案:
【答案】(1)平行;(2)见解析;(3)![]() .
.
【解析】
(1)根据三角形中位线定理得出DE∥BC,DE=![]() BC,FG∥BC,FG=
BC,FG∥BC,FG=![]() BC,那么DE∥FG,DE=FG,利用有一组对边平行且相等的四边形是平行四边形即可得出四边形DEFG是平行四边形;
BC,那么DE∥FG,DE=FG,利用有一组对边平行且相等的四边形是平行四边形即可得出四边形DEFG是平行四边形;
(2)先由矩形的性质得出OD=OE=OF=OG.再根据重心的性质得到OB=2OD,OC=2OE,等量代换得出OB=OC.利用SAS证明△BOE≌△COD,得出BE=CD,然后根据中点的定义即可证明AB=AC;
(3)连接AO并延长交BC于点M,先由三角形中线的性质得出M为BC的中点,由(2)得出AB=AC,根据等腰三角形三线合一的性质得出AM⊥BC,再由三角形中位线定理及三角形重心的性质得出BC=2FG=4,AM=![]() AO=6,由勾股定理求出AB=2
AO=6,由勾股定理求出AB=2![]() ,进而得到△ABC的周长.
,进而得到△ABC的周长.
(1)解:∵△ABC的中线BD,CE交于点O,
∴DE∥BC,DE=![]() BC,
BC,
∵F,G分别是BO,CO的中点,
∴FG∥BC,FG=![]() BC,
BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形.
故答案为平行;
(2)证明:∵四边形DEFG是矩形,
∴OD=OE=OF=OG.
∵△ABC的中线BD,CE交于点O,
∴点O是△ABC的重心,
∴OB=2OD,OC=2OE,
∴OB=OC.
在△BOE与△COD中,
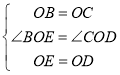 ,
,
∴△BOE≌△COD(SAS),
∴BE=CD,
∵E、D分别是AB、AC中点,
∴AB=AC;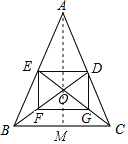
(3)解:连接AO并延长交BC于点M.
∵三角形的三条中线相交于同一点,△ABC的中线BD、CE交于点O,
∴M为BC的中点,
∵四边形DEFG是正方形,
由(2)可知,AB=AC,
∴AM⊥BC.
∵正方形DEFG边长为2,F,G分别是BO,CO的中点,
∴BC=2FG=4,BM=MC=![]() BC=2,AO=2EF=4,
BC=2,AO=2EF=4,
∴AM=![]() AO=6,
AO=6,
∴AB=![]() =
=![]() =2
=2![]() ,
,
∴△ABC的周长=AB+AC+BC=4![]() +4.
+4.
-
科目: 来源: 题型:
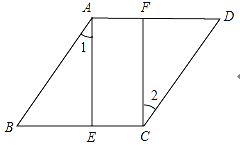
查看答案和解析>>【题目】如图,点E,F在菱形ABCD的对边上,AE⊥BC.∠1=∠2.
(1)判断四边形AECF的形状,并证明你的结论.
(2)若AE=4,AF=2,试求菱形ABCD的面积.
-
科目: 来源: 题型:
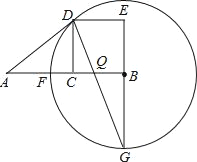
查看答案和解析>>【题目】设C为线段AB的中点,四边形BCDE是以BC为一边的正方形.以B为圆心,BD长为半径的⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
求证:(1)AD是⊙B的切线;(2)AD=AQ;(3)BC2=CFEG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
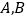 两地相距300
两地相距300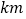 ,甲、乙两车同时从
,甲、乙两车同时从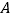 地出发驶向
地出发驶向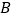 地,甲车到达
地,甲车到达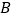 地后立即返回,如图是两车离
地后立即返回,如图是两车离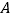 地的距离
地的距离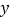 (
(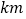 )与行驶时间
)与行驶时间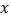 (
(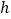 )之间的函数图象.
)之间的函数图象.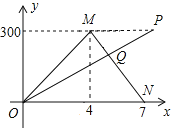
(1)求甲车行驶过程中
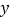 与
与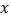 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量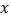 的取值范围.
的取值范围.(2)若两车行驶5
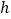 相遇,求乙车的速度.
相遇,求乙车的速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过点A(6,0)的直线y=kx﹣3与直线y=﹣x交于点B,点P从点O出发以每秒1个单位长度的速度向点A匀速运动.
(1)求点B的坐标;
(2)当△OPB是直角三角形时,求点P运动的时间;
(3)当BP平分△OAB的面积时,直线BP与y轴交于点D,求线段BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程ax2﹣2(a﹣1)x+a﹣2=0(a>0).
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2(其中x1>x2).若y是关于a的函数,且y=ax2x1,求这个函数的表达式;
(3)将(2)中所得的函数的图象在直线a=2的左侧部分沿直线a=2翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象直接写出:当关于a的函数y=2a+b的图象与此图象有两个公共点时,b的取值范围是 .
相关试题

