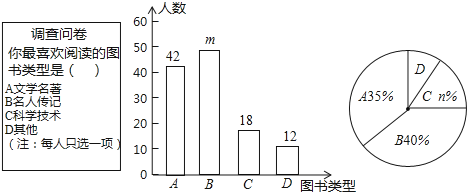
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
(1)本次调查共抽查了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?
参考答案:
【答案】(1)120,48,15;(2)336;(3)![]() .
.
【解析】试题分析:(1)用A类的人数除以所占的百分比求出总人数,用总数减去A,C,D类的人数,即可求出m的值,用C类的人数除以总人数,即可得出n的值;
(2)用该校喜欢阅读“A”类图书的学生人数=学校总人数×A类的百分比求解即可;
(3)列出图形,即可得出答案.
试题解析:(1)这次调查的学生人数为42÷35%=120(人),m=120﹣42﹣18﹣12=48,18÷120=15%;所以n=15,故答案为:120,48,15;
(2)该校喜欢阅读“A”类图书的学生人数为:960×35%=336(人);
(3)抽出的所有情况如图:
![]()
两名参赛同学为1男1女的概率为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<b,则a+c<b+c。()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图1是某仓库的实物图片,图2是该仓库屋顶(虚线部分)的正面示意图,BE、CF关于AD轴对称,且AD、BE、CF都与EF垂直,AD=3米,在B点测得A点的仰角为30°,在E点测得D点的仰角为20°,EF=6米,求BE的长.(结果精确到0.1米,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,
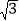 ≈1.73)
≈1.73)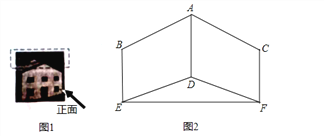
-
科目: 来源: 题型:
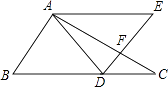
查看答案和解析>>【题目】将一副直角三角尺如图放置,已知AE∥BC,求∠AFD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将方程x2+4x+2=0配方后,原方程变形为( )
A. (x+4)2=2B. (x+2)2=2C. (x+4)2=-3D. (x+2)2=-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的底和腰是方程x2﹣7x+10=0的两根,则这个三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m﹣3)2+n2﹣6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.

(1)求m、n的值并写出A、B、C三点的坐标;
(2)若OF+BE=AB,求证:CF=CE.
相关试题

