【题目】(1)类比计算
①6×12=1×2×3;
②6×22=2×3×5﹣1×2×3;
③6×32=3×4×7﹣2×3×5;
④6×42=4×5×9﹣3×4×7;
⑤ ;
(2)规律提炼
写出第n个式子(用含字母n的式子表示).
(3)问题解决
求12+22+33+42+…+592+602的值.
参考答案:
【答案】(1)5×6×11﹣4×5×9.(2)6n2=n(n+1)(2n+1)﹣(n﹣1)n(2n﹣1).(3)73810.
【解析】
(1)⑤根据题目中前几个式子的规律即可得结论6×52=5×6×11﹣4×5×9;
(2)根据前边几个式子的规律即可写出第n个式子6×n2=n(n+1)(2n+1)﹣(n﹣1)n(2n﹣1).;
(3)先变形为![]() (6×12+6×22+6×32+6×42+…+6×592+6×602),再利用(2)中求得的规律式展开,即可求解.
(6×12+6×22+6×32+6×42+…+6×592+6×602),再利用(2)中求得的规律式展开,即可求解.
解:(1)∵①6×12=1×2×3;
②6×22=2×3×5﹣1×2×3;
③6×32=3×4×7﹣2×3×5;
④6×42=4×5×9﹣3×4×7;
∴⑤6×52=5×6×11﹣4×5×9
故答案为6×52=5×6×11﹣4×5×9.
(2)根据以上算式,得
第n个式子为6n2=n(n+1)(2n+1)﹣(n﹣1)n(2n﹣1).
(3)12+22+33+42+…+592+602
=![]() (6×12+6×22+6×32+6×42+…+6×592+6×602)
(6×12+6×22+6×32+6×42+…+6×592+6×602)
=![]() (1×2×3+2×3×5﹣1×2×3+3×4×7﹣2×3×5+4×5×9﹣3×4×7+…+59×60×119﹣58×59×117+60×61×121﹣59×60×119)
(1×2×3+2×3×5﹣1×2×3+3×4×7﹣2×3×5+4×5×9﹣3×4×7+…+59×60×119﹣58×59×117+60×61×121﹣59×60×119)
=![]() ×60×61×121
×60×61×121
=73810.
答:12+22+33+42+…+592+602的值为73810.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个n位自然数
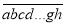 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数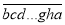 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数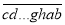 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后, 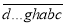 能被x0+3整除,…,
能被x0+3整除,…, 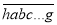 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数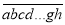 是x0的一个“轮换数”.
是x0的一个“轮换数”.例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2的一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数
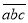 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数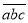 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=﹣
 x2+
x2+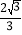 x+
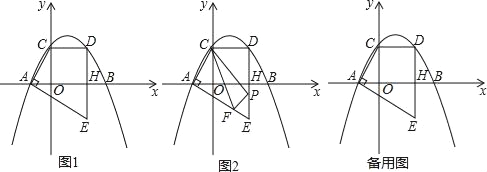
x+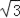 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.(1)求线段DE的长度;
(2)如图2,试在线段AE上找一点F,在线段DE上找一点P,且点M为直线PF上方抛物线上的一点,求当△CPF的周长最小时,△MPF面积的最大值是多少;
(3)在(2)问的条件下,将得到的△CFP沿直线AE平移得到△C′F′P′,将△C′F′P′沿C′P′翻折得到△C′P′F″,记在平移过称中,直线F′P′与x轴交于点K,则是否存在这样的点K,使得△F′F″K为等腰三角形?若存在求出OK的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下
型号
进价(元/只)
售价(元/只)
A型
10
12
B型
15
23
(1)该店用1300元可以购进A,B两种型号的文具各多少只?
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③
 (∠A+∠B)④
(∠A+∠B)④ (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中, AB∥DC,∠BCD=90°,且AB=1,BC=2,
tan∠ADC=2.
(1)求证:DC=BC;
(2)E是梯形内的一点,F是梯形外的一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3)在⑵的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.

相关试题

