【题目】如图1,已知抛物线y=﹣![]() x2+
x2+![]() x+
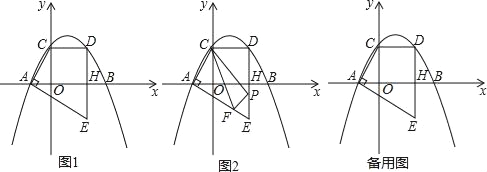
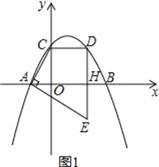
x+![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.
(1)求线段DE的长度;
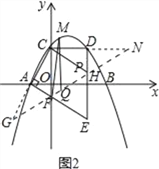
(2)如图2,试在线段AE上找一点F,在线段DE上找一点P,且点M为直线PF上方抛物线上的一点,求当△CPF的周长最小时,△MPF面积的最大值是多少;
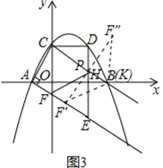
(3)在(2)问的条件下,将得到的△CFP沿直线AE平移得到△C′F′P′,将△C′F′P′沿C′P′翻折得到△C′P′F″,记在平移过称中,直线F′P′与x轴交于点K,则是否存在这样的点K,使得△F′F″K为等腰三角形?若存在求出OK的值;若不存在,说明理由.
参考答案:
【答案】(1)2![]() ;(2)
;(2) ![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)根据解析式求得C的坐标,进而求得D的坐标,即可求得DH的长度,令y=0,求得A,B的坐标,然后证得△ACO∽△EAH,根据对应边成比例求得EH的长,进继而求得DE的长;
(2)找点C关于DE的对称点N(4,![]() ),找点C关于AE的对称点G(-2,-
),找点C关于AE的对称点G(-2,-![]() ),连接GN,交AE于点F,交DE于点P,即G、F、P、N四点共线时,△CPF周长=CF+PF+CP=GF+PF+PN最小,根据点的坐标求得直线GN的解析式:y=
),连接GN,交AE于点F,交DE于点P,即G、F、P、N四点共线时,△CPF周长=CF+PF+CP=GF+PF+PN最小,根据点的坐标求得直线GN的解析式:y=![]() x-
x-![]() ;直线AE的解析式:y= -
;直线AE的解析式:y= -![]() x-
x-![]() ,过点M作y轴的平行线交FH于点Q,设点M(m,-
,过点M作y轴的平行线交FH于点Q,设点M(m,-![]() m+
m+![]() m+
m+![]() ),则Q(m,
),则Q(m,![]() m-
m-![]() ),根据S△MFP=S△MQF+S△MQP,得出S△MFP= -
),根据S△MFP=S△MQF+S△MQP,得出S△MFP= -![]() m+
m+![]() m+
m+![]() ,根据解析式即可求得,△MPF面积的最大值;
,根据解析式即可求得,△MPF面积的最大值;
(3)由(2)可知C(0,![]() ),F(0,
),F(0,![]() ),P(2,
),P(2,![]() ),求得CF=
),求得CF=![]() ,CP=
,CP=![]() ,进而得出△CFP为等边三角形,边长为
,进而得出△CFP为等边三角形,边长为![]() ,翻折之后形成边长为
,翻折之后形成边长为![]() 的菱形C′F′P′F″,且F′F″=4,然后分三种情况讨论求得即可.
的菱形C′F′P′F″,且F′F″=4,然后分三种情况讨论求得即可.
本题解析:(1)对于抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() ,
,
令x=0,得y=![]() ,即C(0,
,即C(0,![]() ),D(2,
),D(2,![]() ),
),
∴DH=![]() ,
,
令y=0,即﹣![]() x2+
x2+![]() x+
x+![]() =0,得x1=﹣1,x2=3,
=0,得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
∵AE⊥AC,EH⊥AH,
∴△ACO∽△EAH,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:EH=![]() ,
,
则DE=2![]() ;
;
(2)找点C关于DE的对称点N(4,![]() ),找点C关于AE的对称点G(﹣2,﹣
),找点C关于AE的对称点G(﹣2,﹣![]() ),
),
连接GN,交AE于点F,交DE于点P,即G、F、P、N四点共线时,△CPF周长=CF+PF+CP=GF+PF+PN最小,
直线GN的解析式:y=![]() x﹣
x﹣![]() ;直线AE的解析式:y=﹣
;直线AE的解析式:y=﹣![]() x﹣
x﹣![]() ,
,
联立得:F (0,﹣![]() ),P(2,
),P(2,![]() ),
),
过点M作y轴的平行线交FH于点Q,
设点M(m,﹣![]() m2+
m2+![]() m+
m+![]() ),则Q(m,
),则Q(m,![]() m﹣
m﹣![]() ),(0<m<2);
),(0<m<2);
∴S△MFP=S△MQF+S△MQP=![]() MQ×2=MQ=﹣
MQ×2=MQ=﹣![]() m2+
m2+![]() m+
m+![]()
![]() ,
,
∵对称轴为:直线m=![]() <2,开口向下,
<2,开口向下,
∴m=![]() 时,△MPF面积有最大值:
时,△MPF面积有最大值:![]()
![]() ;
;
(3)由(2)可知C(0,![]() ),F(0,
),F(0,![]() ),P(2,
),P(2,![]() ),
),
∴CF=![]() ,CP=
,CP=![]() =
=![]() ,
,
∵OC=![]() ,OA=1,
,OA=1,
∴∠OCA=30°,
∵FC=FG,
∴∠OCA=∠FGA=30°,
∴∠CFP=60°,
∴△CFP为等边三角形,边长为![]() ,
,
翻折之后形成边长为![]() 的菱形C′F′P′F″,且F′F″=4,
的菱形C′F′P′F″,且F′F″=4,
1)当K F′=KF″时,如图3,
点K在F′F″的垂直平分线上,所以K与B重合,坐标为(3,0),
∴OK=3;
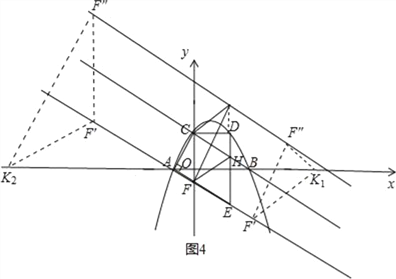
2)当F′F″=F′K时,如图4,
∴F′F″=F′K=4,
∵FP的解析式为:y=![]() x﹣
x﹣![]() ,
,
∴在平移过程中,F′K与x轴的夹角为30°,
∵∠OAF=30°,
∴F′K=F′A
∴AK=4![]()
∴OK=4![]() ﹣1或者4
﹣1或者4![]() +1;
+1;
3)当F″F′=F″K时,如图5,
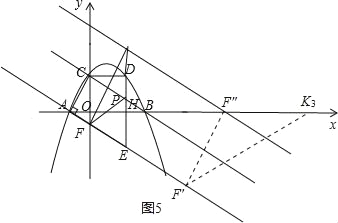
∵在平移过程中,F″F′始终与x轴夹角为60°,
∵∠OAF=30°,
∴∠AF′F″=90°,
∵F″F′=F″K=4,
∴AF″=8,
∴AK=12,
∴OK=11,
综上所述:OK=3,4![]() ﹣1,4
﹣1,4![]() +1或者11.
+1或者11.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“铁路建设助推经济发展”,近年来我国政府十分重视铁路建设.渝利铁路通车后,从重庆到上海比原铁路全程缩短了320千米,列车设计运行时速比原铁路设计运行时速提高了120千米/小时,全程设计运行时间只需8小时,比原铁路设计运行时间少用16小时.
(1)渝利铁路通车后,重庆到上海的列车设计运行里程是多少千米?
(2)专家建议:从安全的角度考虑,实际运行时速减少m%,以便于有充分时间应对突发事件,这样,从重庆到上海的实际运行时间将增加
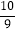 m%小时,求m的值.
m%小时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一个n位自然数
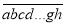 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数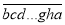 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数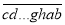 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后, 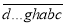 能被x0+3整除,…,
能被x0+3整除,…, 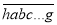 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数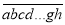 是x0的一个“轮换数”.
是x0的一个“轮换数”.例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2的一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数
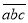 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数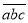 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)类比计算
①6×12=1×2×3;
②6×22=2×3×5﹣1×2×3;
③6×32=3×4×7﹣2×3×5;
④6×42=4×5×9﹣3×4×7;
⑤ ;
(2)规律提炼
写出第n个式子(用含字母n的式子表示).
(3)问题解决
求12+22+33+42+…+592+602的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下
型号
进价(元/只)
售价(元/只)
A型
10
12
B型
15
23
(1)该店用1300元可以购进A,B两种型号的文具各多少只?
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③
 (∠A+∠B)④
(∠A+∠B)④ (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
相关试题

