【题目】如图,在梯形ABCD中, AB∥DC,∠BCD=90°,且AB=1,BC=2,
tan∠ADC=2.
(1)求证:DC=BC;
(2)E是梯形内的一点,F是梯形外的一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3)在⑵的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.

参考答案:
【答案】(1)见解析(2)等腰直角三角形,证明见解析(3)![]()
【解析】
(1)过A点作AG⊥DC,垂足为G,只需求DG+CG,在直角三角形AGD中,可求DG=5,所以DC=BC;
(2)由已知可证△DEC≌△BFC,得EC=CF,∠ECD=∠FCB,由∠BCE+∠ECD=90°得∠ECF=90°,即△ECF是等腰直角三角形;
(3)设BE=k,CE= 2k,由已知,求出∠BEF=90°, 根据勾股定理求出BF=3k,根据锐角三角函数的定义即可求出答案.
解:(1)过A作DC的垂线AM交DC于M,

则AM=BC=2. 又tan∠ADC=2,所以![]() DM=
DM=![]() =1.
=1.
因为MC=AB=1,所以DC=DM+MC=2,即DC=BC.
(2)等腰直角三角形.
证明:因为DE=DF,∠EDC=∠FBC,DC=BC.
所以,△DEC≌△BFC(SAS)
所以,CE=CF,∠ECD=∠BCF.
所以,∠ECF=∠BCF+∠BCE=∠ECD+∠BCE=∠BCD=90°
即△ECF是等腰直角三角形.
(3)设BE=k,则CE=CF=2k,所以![]() .
.
因为∠BEC=135°,又∠CEF=45°,所以∠BEF=90°.
所以![]() 所以
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)类比计算
①6×12=1×2×3;
②6×22=2×3×5﹣1×2×3;
③6×32=3×4×7﹣2×3×5;
④6×42=4×5×9﹣3×4×7;
⑤ ;
(2)规律提炼
写出第n个式子(用含字母n的式子表示).
(3)问题解决
求12+22+33+42+…+592+602的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下
型号
进价(元/只)
售价(元/只)
A型
10
12
B型
15
23
(1)该店用1300元可以购进A,B两种型号的文具各多少只?
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③
 (∠A+∠B)④
(∠A+∠B)④ (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2019=( )
A.(31,47)B.(31,48)C.(32,48)D.(32,49)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,a、b、c 均为非零实数,且 a>b>c,关于 x 的一元二次方程ax2 bx c 0 有两个实数根 x1和 2。(1)4a +2b +c _____0,a _____0,c _________0(填“>”,“=”,“<”)(2)方程 ax2 bx c 0 的另一个根 x1=_______(用含 a、c 的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
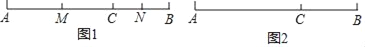
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
相关试题

