搜索
【题目】如图所示，PA、PB是⊙O的切线，A、B为切点，∠APB=80°，点C是⊙O上不同于A、B的任意一点，求∠ACB的度数．
参考答案：
【答案】①若C点在劣弧AB上，则∠ACB=130°；②若C点在优弧AB上，则∠ACB=50°．
【解析】
本题注意要分情况讨论：C点在劣弧AB上或点C点在优弧AB上．连接过切点的半径，根据四边形的内角和定理求得∠AOB的度数，进一步根据圆周角定理进行计算．
连接OA、OB，在AB弧上任取一点C，连接AC、BC．
∵PA、PB是⊙O的切线，A、B为切点，∴∠OAP=∠OBP=90°．
∵∠APB=80°，在四边形OAPB中，可得∠AOB=100°．
分两种情况讨论：
①若C点在劣弧AB上，则∠ACB=130°；
②若C点在优弧AB上，则∠ACB=50°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线AB交x轴于点B（6，0），交y轴于点C（0，6），直线AB与直线OA：y＝
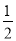x相交于点A，动点M在线段OA和射线AC上运动．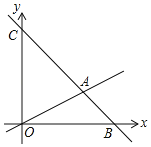
（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）是否存在点M，使△OMC的面积是△OAC的面积的
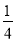？若存在求出此时点M的坐标；若不存在，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，有一个△ABC，顶点
，
，
.
（1）画出△ABC 关于 y 轴的对称图形
（不写画法）点A 关于 x 轴对称的点坐标为_____________；
点 B 关于 y 轴对称的点坐标为_____________；
点 C 关于原点对称的点坐标为_____________；
（2）若网格上的每个小正方形的边长为 1，求△ABC 的面积.
-
科目： 来源： 题型：
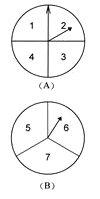
查看答案和解析>>【题目】甲乙两人在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示．游戏规定，转动两个转盘停止后，指针所指的两个数字之和为奇数时，甲获胜；为偶数时，乙获胜．
（1）用列表法（或画树状图）求甲获胜的概率；
（2）你认为这个游戏规则对双方公平吗？请简要说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两位同学5次数学成绩统计如表，他们的5次总成绩相同，小明根据他们的成绩绘制了尚不完整的统计图表，请同学们完成下列问题．
其中，甲的折线图为虚线、乙的折线图为实线．
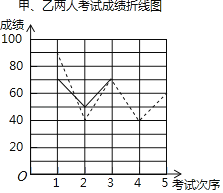
甲、乙两人的数学成绩统计表
第1次
第2次
第3次
第4次
第5次
甲成绩
90
40
70
40
60
乙成绩
70
50
70
a
70
（1）a＝ ，
；（2）请完成图中表示乙成绩变化情况的折线；
（3）S2甲＝260，乙成绩的方差是 ，可看出 的成绩比较稳定（填“甲”或“乙”）．从平均数和方差的角度分析， 将被选中．
-
科目： 来源： 题型：
查看答案和解析>>【题目】水果店张阿姨以每千克4元的价格购进某种水果若干千克，然后以每千克6元的价格出售，每天售出100千克．通过调查发现，这种水果每千克的售价每降低0.1元，每天可多售出20千克，为了保证每天至少售出240千克，张阿姨决定降价销售．
（1）若售价降低0.8元，则每天的销售量为 千克、销售利润为 元；
（2）若将这种水果每千克降价x元，则每天的销售量是 千克（用含x的代数式表示）；
（3）销售这种水果要想每天盈利300元，张阿姨应将每千克的销售价降至多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△OAC中，以O为圆心，OA为半径作⊙O，作OB⊥OC交⊙O于B，垂足为O，连接AB交OC于点D，∠CAD=∠CDA．
（1）判断AC与⊙O的位置关系，并证明你的结论；
（2）若OA=5，OD=1，求线段AC的长．
相关试题
