【题目】如图,在平面直角坐标系中,直线AB交x轴于点B(6,0),交y轴于点C(0,6),直线AB与直线OA:y=![]() x相交于点A,动点M在线段OA和射线AC上运动.
x相交于点A,动点M在线段OA和射线AC上运动.
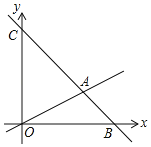
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
参考答案:
【答案】(1)y=﹣x+6;(2)12;(3)存在满足条件的点M,其坐标为(1,![]() )或(1,5)或(﹣1,7)
)或(1,5)或(﹣1,7)
【解析】
(1)由B、C坐标,根据待定系数法可求得直线AB的解析式;
(2)联立直线AB和直线OA解析式可求得A点坐标,则可求得△OAC的面积;
(3)当△OMC的面积是△OAC的面积的![]() 时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
解:(1)设直线AB的解析式是y=kx+b,
根据题意得![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+6;
(2)联立直线OA和直线AB的解析式可得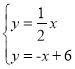 ,解得
,解得![]() ,
,
∴A(4,2),
∴S△OAC=![]() ×6×4=12;
×6×4=12;
(3)由题意可知S△OMC=![]() S△OAC=
S△OAC=![]() ×12=3,
×12=3,
设M点的横坐标为t,则有S△OMC=![]() ×OC|t|=3|t|,
×OC|t|=3|t|,
∴3|t|=3,解得t=1或t=﹣1,
当点t=﹣1时,可知点M在线段AC的延长线上,
∴y=﹣(﹣1)+6=7,此时M点坐标为(﹣1,7);
当点t=1时,可知点M在线段OA或线段AC上,
在y=![]() x中,x=1可得y=
x中,x=1可得y=![]() ,代入y=﹣x+6可得y=5,
,代入y=﹣x+6可得y=5,
∴M的坐标是(1,![]() );
);
在y=﹣x+6中,x=1则y=5,
∴M的坐标是(1,5);
综上可知存在满足条件的点M,其坐标为(1,![]() )或(1,5)或(﹣1,7).
)或(1,5)或(﹣1,7).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
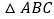 的面积是
的面积是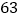 ,
,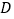 是
是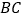 上的一点,且
上的一点,且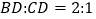 ,
, 交
交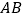 于
于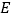 ,延长
,延长 到
到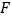 ,使
,使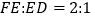 ,则
,则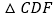 的面积是________.
的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如右表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)根据表格中的数据,计算出甲的平均成绩是________环,乙的平均成绩是________环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
-
科目: 来源: 题型:
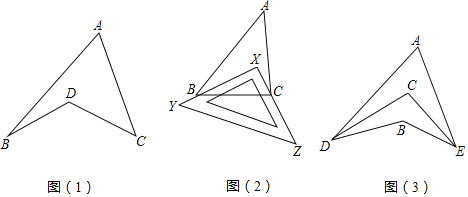
查看答案和解析>>【题目】探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图
(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图(2),把一块三角尺XYZ放置在△ABC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX= °.
②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有一个△ABC,顶点
 ,
, ,
, .
.
(1)画出△ABC 关于 y 轴的对称图形
 (不写画法)
(不写画法)点A 关于 x 轴对称的点坐标为_____________;
点 B 关于 y 轴对称的点坐标为_____________;
点 C 关于原点对称的点坐标为_____________;
(2)若网格上的每个小正方形的边长为 1,求△ABC 的面积.
-
科目: 来源: 题型:
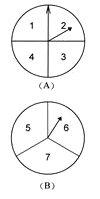
查看答案和解析>>【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=80°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数.

相关试题

