【题目】如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
参考答案:
【答案】(1)线段AC是⊙O的切线。理由见解析(2)12
【解析】
解:(1)线段AC是⊙O的切线。理由如下:
∵∠CAD=∠CDA(已知),∠BDO=∠CDA(对顶角相等),
∴∠BDO=∠CAD(等量代换)。
又∵OA=OB(⊙O的半径),∴∠B=∠OAB(等边对等角)。
∵OB⊥OC(已知),∴∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°。
∴线段AC是⊙O的切线。
(2)设AC=x.
∵∠CAD=∠CDA(已知),∴DC=AC=x(等角对等边)。
∵OA=5,OD=1,∴OC=OD+DC=1+x;
∵由(1)知,AC是⊙O的切线,
∴在Rt△OAC中,根据勾股定理得,OC2=AC2+OA2,即(1+x)2=x2+52,解得x=12。
∴AC=12.
(1)根据已知条件“∠CAD=∠CDA”、对顶角∠BDO=∠CDA可以推知∠BDO=∠CAD;然后根据等腰三角形OAB的两个底角相等、直角三角形的两个锐角互余的性质推知
∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°。所以线段AC是⊙O的切线。
(2)根据“等角对等边”可以推知AC=DC,所以由图形知OC=OD+CD;然后利用(1)中切线的性质可以在在Rt△OAC中,根据勾股定理来求AC的长度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=80°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学5次数学成绩统计如表,他们的5次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.
其中,甲的折线图为虚线、乙的折线图为实线.
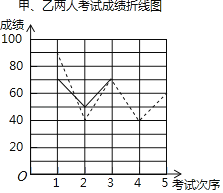
甲、乙两人的数学成绩统计表
第1次
第2次
第3次
第4次
第5次
甲成绩
90
40
70
40
60
乙成绩
70
50
70
a
70
(1)a= ,
 ;
;(2)请完成图中表示乙成绩变化情况的折线;
(3)S2甲=260,乙成绩的方差是 ,可看出 的成绩比较稳定(填“甲”或“乙”).从平均数和方差的角度分析, 将被选中.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店张阿姨以每千克4元的价格购进某种水果若干千克,然后以每千克6元的价格出售,每天售出100千克.通过调查发现,这种水果每千克的售价每降低0.1元,每天可多售出20千克,为了保证每天至少售出240千克,张阿姨决定降价销售.
(1)若售价降低0.8元,则每天的销售量为 千克、销售利润为 元;
(2)若将这种水果每千克降价x元,则每天的销售量是 千克(用含x的代数式表示);
(3)销售这种水果要想每天盈利300元,张阿姨应将每千克的销售价降至多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+2x﹣3.
(1)写出它的顶点坐标;
(2)当x取何值时,y随x的增大而增大;
(3)求出图象与x轴的交点坐标.
(4)当x取何值时y的值大于0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg
0
1
2
3
4
5
y/cm
20
20.5
21
21.5
22
22.5
A. x与y都是变量,且x是自变量,y是x的函数
B. 弹簧不挂重物时的长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为23.5 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面各问题中给出的两个变量x,y,其中y是x的函数的是
① x是正方形的边长,y是这个正方形的面积;
② x是矩形的一边长,y是这个矩形的周长;
③ x是一个正数,y是这个正数的平方根;
④ x是一个正数,y是这个正数的算术平方根.
A. ①②③B. ①②④C. ②④D. ①④
相关试题

