【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(Ⅰ)请写出AF与BE的数量关系与位置关系分别是什么,并证明.
(Ⅱ)如图2,若将条件“两个等边三角形ADE和DCF”变为两个等腰三角形ADE和DCF,且EA=ED=FD=FC,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
参考答案:
【答案】试题
【解析】(Ⅰ)AF=BE,AF⊥BE. 证明参考(Ⅱ)
(Ⅱ)结论成立. 
证明:∵四边形ABCD是正方形,
∴BA=AD =DC,∠BAD =∠ADC = 90°.
在△EAD和△FDC中, 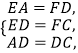
∴△EAD≌△FDC.
∴∠EAD=∠FDC.
∴∠EAD+∠DAB=∠FDC+∠CDA,即∠BAE=∠ADF.
在△BAE和△ADF中, 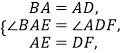
∴△BAE≌△ADF.
∴BE = AF,∠ABE=∠DAF.
∵∠DAF +∠BAF=90°,
∴∠ABE +∠BAF=90°,
∴AF⊥BE.
(Ⅰ)根据SAS易证△ADE≌△DCF,即可证明AF与BE的数量关系是AF=BE,位置关系是AF⊥BE; (Ⅱ)成立,证明△ADE≌△DCF,然后证明△ABE≌△ADF即可证得BE=AF,然后根据三角形内角和定理证明∠AMB=90°,从而结论得证.
【考点精析】关于本题考查的三角形的内角和外角,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=1是一元二次方程x2﹣a=0的一个根,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AB=AC,AD是△ABC的角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,M,F.若∠CAD=20°,求∠MCD的度数.
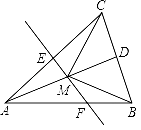
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由一些火彩棒搭成的图案:
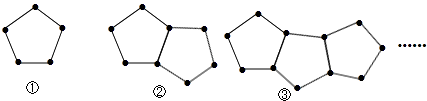
(1)摆第①个图案用根火柴棒;
摆第②个图案用根火柴棒;
摆第③个图案用根火柴棒;
摆第④个图案用根火柴棒;
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?摆第2015个图案需要用多少根火柴棒? -
科目: 来源: 题型:
查看答案和解析>>【题目】下面比较,正确的是( )
A. ﹣24<(﹣2)2<(﹣2)3 B. (﹣2)2<(﹣2)3<﹣24
C. (﹣2)3<﹣24<(﹣2)2 D. ﹣24<(﹣2)3<(﹣2)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
(1)①当PC∥QB时,OQ= ;
②当PC⊥QB时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=
 的图象交于A、B两点,则四边形MAOB的面积为________.
的图象交于A、B两点,则四边形MAOB的面积为________.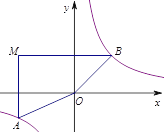
相关试题

