【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
(1)①当PC∥QB时,OQ= ;
②当PC⊥QB时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.

参考答案:
【答案】(1) 2 (2)2![]() +2 , 2
+2 , 2![]() -2 (3)符合条件的点Q共有5个. ①当点C在∠AOB内部或一边上时,OQ=2,
-2 (3)符合条件的点Q共有5个. ①当点C在∠AOB内部或一边上时,OQ=2,![]() ,2
,2![]() ②当点C在∠AOB的外部时,OQ=
②当点C在∠AOB的外部时,OQ=![]() +
+![]() ,
,![]() -
-![]() .
.
【解析】试题分析:(1)①由平行线的性质得出∠O=∠CPA,由折叠的性质得出∠C=∠O,OP=CP,证出∠CPA=∠C,得出OP∥QC,证出四边形OPCQ是菱形,得出OQ=OP=2cm即可;
②当PC⊥QB时,分两种情况:设OQ=xcm,证出△OPM是等腰直角三角形,得出OM=![]() ,证出△CQM是等腰直角三角形,得出
,证出△CQM是等腰直角三角形,得出![]() ,得出方程
,得出方程![]() 解方程即可;(ii)同(i)得出:
解方程即可;(ii)同(i)得出:![]() ,即可得出结论;
,即可得出结论;
(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;点C在∠AOB的内部或一边上时,由折叠的性质、三角形内角和定理以及解直角三角形即可求出OQ的长;点C在∠AOB的外部时,同理求出OQ的长即可;
试题解析:
(1)①当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
②当PC⊥QB时,分两种情况:
如图1所示:设OQ=xcm,
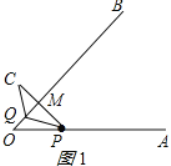
∵∠O=45°,
∴△OPM是等腰直角三角形,
∴OM=![]() ,
,
∴QM=![]() ,
,
由折叠的性质得:∠C=∠O=45°,CQ=OQ=x,
∴△CQM是等腰直角三角形,
∴QC=![]() ,
,
∴![]() ,
,
解得:![]() ,
,
即OQ=![]() ;
;
(ii)如图2所示:
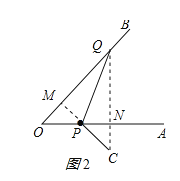
同(i)得:OQ=![]() ,
,
综上所述:当PC⊥QB时,OQ的长为![]() 或
或![]() ;
;
(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;
①点C在∠AOB的内部时,四边形OPCQ是菱形,OQ=OP=2cm;
②当点C在∠AOB的一边上时,△OPQ是等腰直角三角形,OQ=![]() 或
或![]() ,
,
③当点C在∠AOB的外部时,分两种情况:
(i)如图3所示:PM=PQ,则∠PMQ=∠PQM=∠O+∠OPQ,
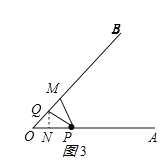
由折叠的性质得:∠OPQ=∠MPQ,
设∠OPQ=∠MPQ=x,
则∠PMQ=∠PQM=45°+x,
在△OPM中,由三角形内角和定理得:45°+x+x+45°+x=180°,
解得:x=30°,
∴∠OPQ=30°,
作QN⊥OP于N,设ON=a,
∵∠O=45°,
则QN=ON=a,OQ=![]() ,PN=
,PN=![]() ,
,
∵ON+PN=OP,
∴a+![]() ,
,
解得:![]() ,
,
∴OQ=![]() ;
;
(ii)如图4所示:PQ=MQ,作QN⊥OA于N,
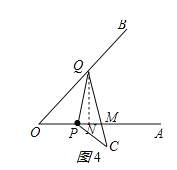
同①得:OQ=![]() ;
;
综上所述:当折叠后重叠部分为等腰三角形时,OQ的长为2cm或![]()
![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由一些火彩棒搭成的图案:
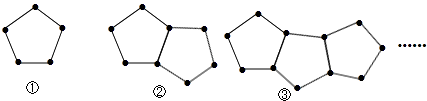
(1)摆第①个图案用根火柴棒;
摆第②个图案用根火柴棒;
摆第③个图案用根火柴棒;
摆第④个图案用根火柴棒;
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?摆第2015个图案需要用多少根火柴棒? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(Ⅰ)请写出AF与BE的数量关系与位置关系分别是什么,并证明.
(Ⅱ)如图2,若将条件“两个等边三角形ADE和DCF”变为两个等腰三角形ADE和DCF,且EA=ED=FD=FC,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面比较,正确的是( )
A. ﹣24<(﹣2)2<(﹣2)3 B. (﹣2)2<(﹣2)3<﹣24
C. (﹣2)3<﹣24<(﹣2)2 D. ﹣24<(﹣2)3<(﹣2)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=
 的图象交于A、B两点,则四边形MAOB的面积为________.
的图象交于A、B两点,则四边形MAOB的面积为________.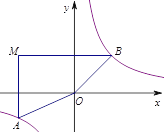
-
科目: 来源: 题型:
查看答案和解析>>【题目】直接写出结果
(1)﹣8﹣2=
(2)2.5﹣(﹣7.5)=
(3) ﹣1=
﹣1=
(4)12÷(- )=
)=
(5)(﹣0.8)×(﹣2)=
(6)(﹣2)3= -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)0﹣16+(﹣29)﹣(﹣7)﹣(+11)
(2)
(3)( )×(﹣30)
)×(﹣30)
(4)
(5) .
.
相关试题

