【题目】抛物线y1=ax2+c与x轴交于A、B两点,与y轴交于点C,点P在抛物线上,过P(1,﹣3),B(4,0)两点作直线y2=kx+b.
(1)求a、c的值;
(2)根据图象直接写出y1>y2时,x的取值范围;
(3)在抛物线上是否存在点M,使得S△ABP=5S△ABM,若存在,求出点M的坐标,若不存在,请说明理由.

参考答案:
【答案】(1)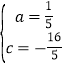 ;(2)x>4或x<1;(3)M点的坐标是(
;(2)x>4或x<1;(3)M点的坐标是(![]() ,
,![]() )(﹣
)(﹣![]() ,
,![]() )(
)(![]() ,﹣
,﹣![]() )(﹣
)(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
由B、P两点的坐标,利用待定系数法可求得a、c;以P、B的横坐标为分界点,直接写出y1>y2时x的取值范围;假定M点的纵坐标为e,根据S△ABP=5S△ABM,可求出M的坐标.
(1)将P(1,﹣3)、B(4,0)代入y=ax2+c得:![]() ,
,
解得: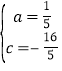 ;
;
(2)由图象得x>4或x<1;
(3)在抛物线上存在点M,使得S△ABP=5S△ABM,
理由是:抛物线的解析式是y=![]() x2﹣
x2﹣![]() ,
,
设M点的纵坐标为e,
∵P(1,﹣3),
∴由S△ABP=5S△ABM得:![]() ×AB×|﹣3|=5×
×AB×|﹣3|=5×![]() ×AB×|e|,
×AB×|e|,
解得;|e|=![]() ,
,
当e=![]() 时,
时,![]() x2﹣
x2﹣![]() =
=![]() ,
,
解得:x=±![]() ,
,
当e=﹣![]() 时,
时,![]() x2﹣
x2﹣![]() =﹣
=﹣![]() ,
,
解得:x=±![]() ,
,
即M点的坐标是(![]() ,
,![]() )(﹣
)(﹣![]() ,
,![]() )(
)(![]() ,﹣
,﹣![]() )(﹣
)(﹣![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,点A、B为函数L图象上的任意两点,点A坐标为(x1,y1),点B坐标为(x2,y2),把式子
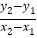 称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=
称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1= 时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=
时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=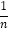 (n为正整数)时,函数K从x1到x2的平均变化率是_____.
(n为正整数)时,函数K从x1到x2的平均变化率是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程.
(1)x2﹣14x=8(配方法)
(2)x2﹣7x﹣18=0(公式法)
(3)(2x+3)2=4(2x+3)(因式分解法)
(4)2(x﹣3)2=x2﹣9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区2015年投入教育经费2900万元,2017年投入教育经费3509万元.
(1)求2015年至2017年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的情况,该地区到2019年需投入教育经费4250万元.如果按(1)中教育经费投入的增长率,到2019年该地区投入的教育经费是否能达到4250万元?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

-
科目: 来源: 题型:
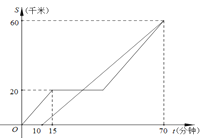
查看答案和解析>>【题目】甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
(1)甲、乙两车行驶时的速度分别为多少?
(2)乙车出发多少分钟后第一次与甲车相遇?
(3)甲车中途因故障停止行驶的时间为多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线
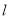 分别交x轴、y轴于A、B两点(AOAB)且AO、AB的长分别是一元二次方程x23x20的两个根,点C在x轴负半轴上,且AB:AC=1:2.
分别交x轴、y轴于A、B两点(AOAB)且AO、AB的长分别是一元二次方程x23x20的两个根,点C在x轴负半轴上,且AB:AC=1:2.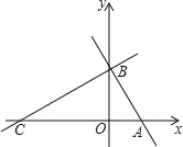
(1)求A、C两点的坐标;
(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.
相关试题

