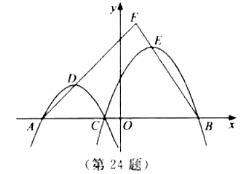
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点(与
上一点(与![]() ,
,![]() 点不重合),抛物线
点不重合),抛物线![]()
![]() (
(![]() )经过点
)经过点![]() ,
,![]() ,顶点为
,顶点为![]() ,抛物线
,抛物线![]()
![]() (
(![]() )经过点
)经过点![]() ,
,![]() ,顶点为
,顶点为![]() ,
,![]() ,
,![]() 的延长线相交于点
的延长线相交于点![]() .
.
(1)若![]() ,
,![]() ,求抛物线
,求抛物线![]() ,
,![]() 的解析式;
的解析式;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)是否存在这样的实数![]() (
(![]() ),无论
),无论![]() 取何值,直线
取何值,直线![]() 与
与![]() 都不可能互相垂直?若存在,请直接写出
都不可能互相垂直?若存在,请直接写出![]() 的两个不同的值;若不存在,请说明理由.
的两个不同的值;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线L1的解析式为y=![]() ,抛物线L2的解析式为y=
,抛物线L2的解析式为y=![]() (2)m=±2
(2)m=±2![]() (3)存在
(3)存在
【解析】
试题分析:(1)把a、m代入得到已知点,把点代入函数的解析式,然后构成方程组,根据待定系数法可求出函数的解析式;
(2)如图,过点D作DG⊥x轴于点G,过点E作EH⊥x轴于点H,把a=-1代入函数解析式,然后结合(m,0)和(-4,0)代入可求解出函数解析式L1,然后分别求出D点坐标,得到DG、AG的长,同理得到L2,求得EH,BH的长,再根据三角形相似的判定与性质构造方程求解即可;
(3)根据前面的解答,直接写出即可.
试题解析:(1)由题意得
解得
所以抛物线L1的解析式为y=![]()
同理,
解得
∴所以抛物线L2的解析式为y=![]()
(2)如图,过点D作DG⊥x轴于点G,过点E作EH⊥x轴于点H
由题意得
解得
∴抛物线L1的解析式为y=-x2+(m-4)x+4m
∴点D的坐标为(![]() ,
,![]() )
)
∴DG=![]() ,AG=
,AG=![]()
同理可得,抛物线L2的解析式为y=-x2+(m+4)x-4m
EH=![]() ,BH=
,BH=![]()

∵AF⊥BF,DG⊥x轴,EH⊥x轴
∴∠AFB=∠AGD=∠EHB=90°
∴∠ADG=∠ABF=90°-∠BAF
∴△ADG∽△EBH
∴![]()
∴
解得m=±2![]()
(3)存在,例如:a=-![]() ,a=-
,a=-![]() .(答案不唯一)
.(答案不唯一)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离
 (千米)与行驶时间
(千米)与行驶时间 (小时)的对应关系如图所示:
(小时)的对应关系如图所示:
(1)甲乙两地相距多远?
(2)求快车和慢车的速度分别是多少?
(3)求出两车相遇后
 与
与 之间的函数关系式;
之间的函数关系式;(4)何时两车相距
 千米.
千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】一艘渔船位于港口
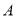 的北偏东
的北偏东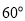 方向,距离港口
方向,距离港口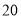 海里
海里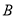 处,它沿北偏西
处,它沿北偏西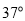 方向航行至
方向航行至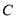 处突然出现故障,在
处突然出现故障,在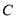 处等待救援,
处等待救援,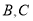 之间的距离为
之间的距离为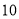 海里,救援船从港口
海里,救援船从港口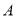 出发
出发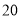 分钟到达
分钟到达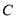 处,求救援的艇的航行速度.
处,求救援的艇的航行速度.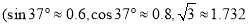 ,结果取整数)
,结果取整数)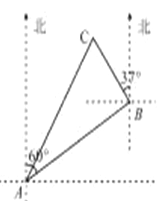
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是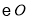 的直径,
的直径,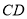 与
与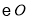 相切于点
相切于点 ,与
,与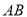 的延长线交于
的延长线交于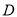 .
.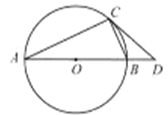
(1)求证:
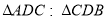 ;
;(2)若
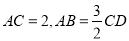 ,求
,求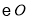 半径.
半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】为积极创建全国文明城市,某市对某路口的行人交通违章情况进行了
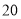 天的调查,将所得数据绘制成如下统计图(图2不完整):
天的调查,将所得数据绘制成如下统计图(图2不完整):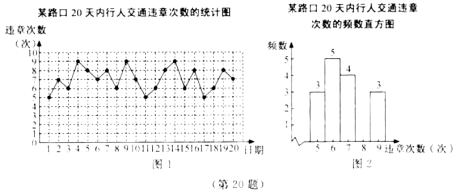
请根据所给信息,解答下列问题:
(1)第
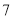 天,这一路口的行人交通违章次数是多少次?这
天,这一路口的行人交通违章次数是多少次?这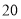 天中,行人交通违章
天中,行人交通违章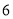 次的有多少天?
次的有多少天?(2)请把图2中的频数直方图补充完整;(温馨提示:请画在答题卷相对应的图上)
(3)通过宣传教育后,行人的交通违章次数明显减少.经对这一路口的再次调查发现,平均每天的行人交通违章次数比第一次调查时减少了
 次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x,-4)与点B(3,y)关于y轴对称,那么x+y的值为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣4x+5的顶点坐标为( )
A.(﹣2,﹣1)
B.(2,1)
C.(2,﹣1)
D.(﹣2,1)
相关试题

