【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 与
与![]() 相切于点
相切于点![]() ,与
,与![]() 的延长线交于
的延长线交于![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 半径.
半径.
参考答案:
【答案】(1)证明见解析;(2)⊙O半径是![]() .
.
【解析】
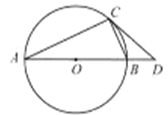
试题分析:(1)首先连接CO,根据CD与⊙O相切于点C,可得:∠OCD=90°;然后根据AB是圆O的直径,可得:∠ACB=90°,据此判断出∠CAD=∠BCD,即可推得△ADC∽△CDB.
(2)首先设CD为x,则AB=![]() x,OC=OB=
x,OC=OB=![]() x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得:
x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得:![]() ,据此求出CB的值是多少,即可求出⊙O半径是多少.
,据此求出CB的值是多少,即可求出⊙O半径是多少.
试题解析:(1)证明:如图,连接CO,
 ,
,
∵CD与⊙O相切于点C,
∴∠OCD=90°,
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠ACO=∠BCD,
∵∠ACO=∠CAD,
∴∠CAD=∠BCD,
在△ADC和△CDB中,
![]()
∴△ADC∽△CDB.
(2)解:设CD为x,
则AB=![]() x,OC=OB=
x,OC=OB=![]() x,
x,
∵∠OCD=90°,
∴OD=![]() ,
,
∴BD=OD﹣OB=![]() ,
,
由(1)知,△ADC∽△CDB,
∴![]() ,
,
即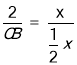 ,
,
解得CB=1,
∴AB=![]() ,
,
∴⊙O半径是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市
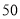 名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):步数
频数
频率
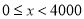
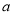
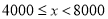
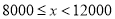
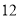
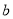
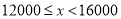
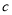
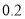
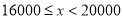
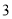
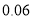

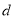
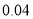
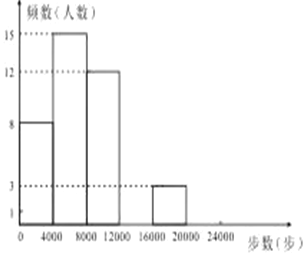
请根据以上信息,解答下列问题:
(1)写出
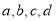 的值并补全频数分布直方图;
的值并补全频数分布直方图;(2)本市约有
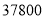 名教师,用调查的样本数据估计日行走步数超过
名教师,用调查的样本数据估计日行走步数超过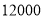 步(包含
步(包含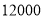 步)的教师有多少名?
步)的教师有多少名?(3)若在
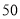 名被调查的教师中,选取日行走步数超过
名被调查的教师中,选取日行走步数超过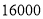 步(包含
步(包含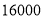 步的两名教师与大家分享心得,求被选取的两名教师恰好都在
步的两名教师与大家分享心得,求被选取的两名教师恰好都在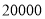 步(包含
步(包含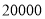 步)以上的概率.
步)以上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离
 (千米)与行驶时间
(千米)与行驶时间 (小时)的对应关系如图所示:
(小时)的对应关系如图所示:
(1)甲乙两地相距多远?
(2)求快车和慢车的速度分别是多少?
(3)求出两车相遇后
 与
与 之间的函数关系式;
之间的函数关系式;(4)何时两车相距
 千米.
千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】一艘渔船位于港口
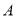 的北偏东
的北偏东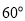 方向,距离港口
方向,距离港口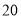 海里
海里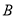 处,它沿北偏西
处,它沿北偏西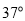 方向航行至
方向航行至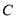 处突然出现故障,在
处突然出现故障,在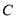 处等待救援,
处等待救援,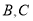 之间的距离为
之间的距离为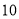 海里,救援船从港口
海里,救援船从港口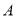 出发
出发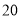 分钟到达
分钟到达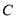 处,求救援的艇的航行速度.
处,求救援的艇的航行速度.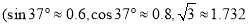 ,结果取整数)
,结果取整数)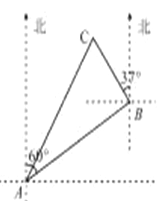
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,已知
中,已知 ,
, 两点的坐标分别为
两点的坐标分别为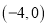 ,
,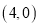 ,
,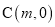 是线段
是线段 上一点(与
上一点(与 ,
, 点不重合),抛物线
点不重合),抛物线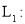
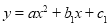 (
(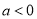 )经过点
)经过点 ,
, ,顶点为
,顶点为 ,抛物线
,抛物线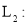
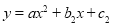 (
(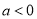 )经过点
)经过点 ,
, ,顶点为
,顶点为 ,
,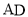 ,
,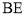 的延长线相交于点
的延长线相交于点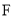 .
.(1)若
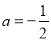 ,
, ,求抛物线
,求抛物线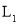 ,
, 的解析式;
的解析式;(2)若
 ,
, ,求
,求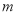 的值;
的值;(3)是否存在这样的实数
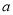 (
(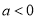 ),无论
),无论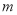 取何值,直线
取何值,直线 与
与 都不可能互相垂直?若存在,请直接写出
都不可能互相垂直?若存在,请直接写出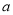 的两个不同的值;若不存在,请说明理由.
的两个不同的值;若不存在,请说明理由.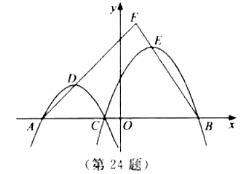
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极创建全国文明城市,某市对某路口的行人交通违章情况进行了
 天的调查,将所得数据绘制成如下统计图(图2不完整):
天的调查,将所得数据绘制成如下统计图(图2不完整):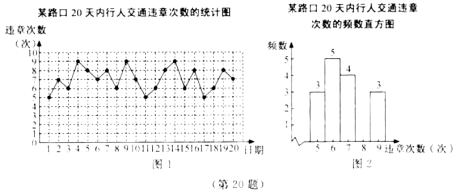
请根据所给信息,解答下列问题:
(1)第
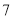 天,这一路口的行人交通违章次数是多少次?这
天,这一路口的行人交通违章次数是多少次?这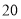 天中,行人交通违章
天中,行人交通违章 次的有多少天?
次的有多少天?(2)请把图2中的频数直方图补充完整;(温馨提示:请画在答题卷相对应的图上)
(3)通过宣传教育后,行人的交通违章次数明显减少.经对这一路口的再次调查发现,平均每天的行人交通违章次数比第一次调查时减少了
 次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x,-4)与点B(3,y)关于y轴对称,那么x+y的值为_______.
相关试题

