Question

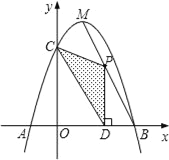
【题目】如图，抛物线y=﹣x2+bx+c与x轴相交于A、B两点，与y轴相交于点C，且点B与点C的坐标分别为B（3，0）．C（0，3），点M是抛物线的顶点．

（1）求二次函数的关系式；

（2）点P为线段MB上一个动点，过点P作PD⊥x轴于点D．若OD=m，△PCD的面积为S，试判断S有最大值或最小值？并说明理由；

（3）在MB上是否存在点P，使△PCD为直角三角形？如果存在，请求出点P的坐标；如果不存在，请说明理由．

Answer 1

【答案】（1）解析式为y=﹣x2+2x+3；（2）当m=时，S有最大值，最大值为； （3）存在，P点坐标为（，3）或（﹣3+3，12﹣6）时，△PCD为直角三角形．

【解析】试题分析：（1）把B点和C点坐标代入y=﹣x2+bx+c得到关于b、c的方程组，然后解方程组求出b、c即可得到抛物线解析式；

（2）把（1）中的一般式配成顶点式可得到M（1，4），设直线BM的解析式为y=kx+n，再利用待定系数法求出直线BM的解析式，则P（m，﹣2m+6）（1≤m＜3），于是根据三角形面积公式得到S=﹣m2+3m，然后根据二次函数的性质解决问题；

（3）讨论：∠PDC不可能为90°；当∠DPC=90°时，易得﹣2m+6=3，解方程求出m即可得到此时P点坐标；当∠PCD=90°时，利用勾股定理得到和两点间的距离公式得到m2+（﹣2m+3）2+32+m2=（﹣2m+6）2，

然后解方程求出满足条件的m的值即可得到此时P点坐标．

试题解析：（1）把B（3，0），C（0，3）代入y=﹣x2+bx+c得，解得，

所以抛物线解析式为y=﹣x2+2x+3；

（2）S有最大值．理由如下：

∵y=﹣x2+2x+3=﹣（x﹣1）2+4，

∴M（1，4），

设直线BM的解析式为y=kx+n，

把B（3，0），M（1，4）代入得，解得，

∴直线BM的解析式为y=﹣2x+6，

∵OD=m，

∴P（m，﹣2m+6）（1≤m＜3），

∴S=m（﹣2m+6）=﹣m2+3m=﹣（m﹣）2+，

∵1≤m＜3，

∴当m=时，S有最大值，最大值为；

（3）存在．

∠PDC不可能为90°；

当∠DPC=90°时，则PD=OC=3，即﹣2m+6=3，解得m=，此时P点坐标为（，3），

当∠PCD=90°时，则PC2+CD2=PD2，即m2+（﹣2m+3）2+32+m2=（﹣2m+6）2，

整理得m2+6m﹣9=0，解得m1=﹣3﹣3（舍去），m2=﹣3+3，

当m=﹣3+3时，y=﹣2m+6=6﹣6+6=12﹣6，此时P点坐标为（﹣3+3，12﹣6），

综上所述，当P点坐标为（，3）或（﹣3+3，12﹣6）时，△PCD为直角三角形．