【题目】在平面直角坐标系xOy中,抛物线y=x2﹣4x+3与x轴交于点A、B(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的表达式;
(2)垂直于y轴的直线l与抛物线交于点P(x1,y1),Q(x2,y2),与直线BC交于点N(x3,y3),若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.
参考答案:
【答案】(1)直线BC的表达式为y=﹣x+3;(2)7<x1+x2+x3<8.
【解析】试题分析:(1)根据抛物线解析式求出点B、C的坐标,然后利用待定系数法即可求出直线BC的表达式;
(2)先求出抛物线的对称轴,顶点坐标,结合图形即可得.
试题解析:(1)由y=x2﹣4x+3得到:y=(x﹣3)(x﹣1),C(0,3).
所以A(1,0),B(3,0),
设直线BC的表达式为:y=kx+b(k≠0),
则![]() ,解得
,解得![]() ,
,
所以直线BC的表达式为y=﹣x+3;
(2)由y=x2﹣4x+3得到:y=(x﹣2)2﹣1,
所以抛物线y=x2﹣4x+3的对称轴是x=2,顶点坐标是(2,﹣1).
∵y1=y2,
∴x1+x2=4.
令y=﹣1,y=﹣x+3,x=4.
∵x1<x2<x3,
∴3<x3<4,即7<x1+x2+x3<8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:若
 =(a,b),
=(a,b), =(c,d),则
=(c,d),则 ·
· =ac+bd.如
=ac+bd.如 =(1,2),
=(1,2), =(3,5),则
=(3,5),则 ·
· =1×3+2×5=13.
=1×3+2×5=13.(1)已知
 =(2,4),
=(2,4), =(2,-3),求
=(2,-3),求 ·
· ;
;(2)已知
 =(x-1,1),
=(x-1,1), =(x-1,x+1),求y=
=(x-1,x+1),求y= ·
· ;
;(3)判断y=
 ·
· 的函数图象与一次函数y=x-1的图象是否相交,请说明理由.
的函数图象与一次函数y=x-1的图象是否相交,请说明理由. -
科目: 来源: 题型:
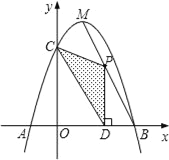
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=3是关于x的方程kx+b=0(k≠0,b>0)的解,则关于x的不等式k(x-4)+b>0的解集是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两队进行足球对抗赛,比赛的规则规定每队胜一场得3分,平一场得1分,负一场得0分.两队一共进行10场比赛,甲队未负一场,得分超过22分.甲队至少胜了多少场?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )

A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.﹣a(a﹣b)=﹣a2﹣ab
B.(2ab)2+a2b=4ab
C.2ab3a=6a2b
D.(a﹣1)(1﹣a)=a2﹣1
相关试题

