【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.

参考答案:
【答案】(1)证明详见解析;(2)9![]() .
.
【解析】试题分析:(1)、根据两组对边分别平行得出平行四边形,根据菱形的性质得出矩形;(2)、根据菱形得出△ABC为正三角形,得出OB和AO的长度,然后计算面积.
试题解析:(1)、∵四边形ABCD是菱形 ∴AC⊥BD,即∠AOD=90° ∵DE∥AC,AE∥BD
∴四边形AODE是平行四边形 ∵∠AOD=90° ∴□AODE是矩形
(2)、∵四边形ABCD是菱形 ∴AO=OC=![]() ,BO=OD,AB=BC, AB∥CD
,BO=OD,AB=BC, AB∥CD
∴∠ABC+∠BCD=180° ∵∠BCD=120° ∴∠ABC=60° ∴△ABC是等边三角形
∴AC=AB=6 ∴OA=3 根据Rt△ABO的勾股定理可得BO=3![]() 即DO=3
即DO=3![]()
∴S=AO×DO=3×3![]() =9
=9![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果:(kam﹣nbm+n)4=16a8b16 , 则k+m+n=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一次函数y=2x﹣3的图象沿y轴向上平移3个单位长度,所得直线的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是
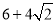 ,其中正确的结论个数为( )
,其中正确的结论个数为( )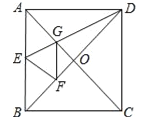
A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列性质中,平行四边形不一定具备的是( )
A.邻角互补
B.对角互补
C.对边相等
D.对角线互相平分 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果m是一个有理数,那么-m是( )。
A、正数 B、0 C、负数 D、以上三者情况都有可能
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是方程x2+x-2009=0的两个实数根,则a+b的值为 ( )
A. 1 B. -1 C. -2009 D. 2009
相关试题

