【题目】等边三角形![]() 的边长为
的边长为![]() ,将其放置在如图所示的平面直角坐标系中,其中
,将其放置在如图所示的平面直角坐标系中,其中![]() 边在
边在![]() 轴上,
轴上,![]() 边的高
边的高![]() 在
在![]() 轴上.一只电子虫从
轴上.一只电子虫从![]() 出发,先沿
出发,先沿![]() 轴到达
轴到达![]() 点,再沿
点,再沿![]() 到达
到达![]() 点,已知电子虫在
点,已知电子虫在![]() 轴上运动的速度是在
轴上运动的速度是在![]() 上运动速度的
上运动速度的![]() 倍,若电子虫走完全程的时间最短,则点
倍,若电子虫走完全程的时间最短,则点![]() 的坐标为________.
的坐标为________.

参考答案:
【答案】![]()
【解析】
如图作GM⊥AB于M,设电子虫在CG上的速度为v,电子虫走完全全程的时间t=![]() ,在Rt△AMG中,GM=
,在Rt△AMG中,GM=![]() AG,TC 电子虫走完全全程的时间t=
AG,TC 电子虫走完全全程的时间t=![]() (GM+CG),当C、G、M共线时,且CM⊥AB时,GM+CG最短,由此即可解决问题.
(GM+CG),当C、G、M共线时,且CM⊥AB时,GM+CG最短,由此即可解决问题.
如图作GM⊥AB于M,
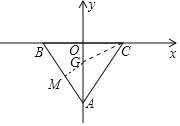
设电子虫在CG上的速度为v,
电子虫走完全全程的时间t=![]() ,
,
在Rt△AMG中,GM=![]() AG,
AG,
∴电子虫走完全全程的时间t=![]() (GM+CG),
(GM+CG),
当C、G、M共线时,且CM⊥AB时,GM+CG最短,
此时CG=AG=2OG,易知OG=![]()
![]() ×6=
×6=![]() ,
,
所以点G的坐标为(0,-![]() ).
).
故答案为:(0,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点分别落在边长为1的正方形格上,
(1)分别写出A、B、C三点坐标;
(2)△DEF可以看作是△ABC经过若干次的图形变化(轴对称、平移)得到的,写出一种由△ABC得到△DEF的过程,并体现在坐标系中.

-
科目: 来源: 题型:
查看答案和解析>>【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件
 元,售价为每件
元,售价为每件 元,每月可卖出
元,每月可卖出 件.市场调查反映:调整价格时,售价每涨
件.市场调查反映:调整价格时,售价每涨 元每月要少卖
元每月要少卖 件;售价每下降
件;售价每下降 元每月要多卖
元每月要多卖 件.为了获得更大的利润,现将饰品售价调整为
件.为了获得更大的利润,现将饰品售价调整为 (元/件)(
(元/件)( 即售价上涨,
即售价上涨, 即售价下降),每月饰品销量为
即售价下降),每月饰品销量为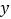 (件),月利润为
(件),月利润为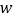 (元).
(元).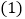 直接写出
直接写出 与
与 之间的函数关系式;
之间的函数关系式; 如何确定销售价格才能使月利润最大?求最大月利润;
如何确定销售价格才能使月利润最大?求最大月利润; 为了使每月利润不少于
为了使每月利润不少于 元应如何控制销售价格?
元应如何控制销售价格? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
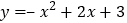 ,
, 画出二次函数
画出二次函数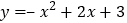 的图象,并根据图象说明,当
的图象,并根据图象说明,当 取何值时,图象位于
取何值时,图象位于 上方?
上方? 请说明经过怎样平移函数
请说明经过怎样平移函数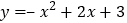 的图象得到函数
的图象得到函数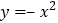 的图象.
的图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的方程
的方程
 若方程有两个有理数根,求整数
若方程有两个有理数根,求整数 的值
的值 若
若 满足不等式
满足不等式 ,试讨论方程根的情况.
,试讨论方程根的情况. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,进价是
 元,根据市场调查:在一段时间内,销售单价是
元,根据市场调查:在一段时间内,销售单价是 元时,销售量是
元时,销售量是 件,而销售单价每涨
件,而销售单价每涨 元,就会少售出
元,就会少售出 件玩具.
件玩具. 不妨设该种品牌玩具的销售单价为
不妨设该种品牌玩具的销售单价为 元
元 ,请你分别用
,请你分别用 的代数式来表示销售量
的代数式来表示销售量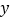 件和销售该品牌玩具获得利润
件和销售该品牌玩具获得利润 元,并把结果填写在表格中:
元,并把结果填写在表格中:销售单价(元)

销售量
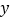 (件)
(件)________
销售玩具获得利润
 (元)
(元)________
 在
在 问条件下,若商场获得了
问条件下,若商场获得了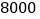 元销售利润,求该玩具销售单价
元销售利润,求该玩具销售单价 应定为多少元.
应定为多少元. 在
在 问条件下,若玩具厂规定该品牌玩具销售单价不低于
问条件下,若玩具厂规定该品牌玩具销售单价不低于 元,且商场要完成不少于
元,且商场要完成不少于 件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
件的销售任务,求商场销售该品牌玩具获得的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在
 中,
中, ,
, ,
, ,点
,点 从点
从点 开始沿
开始沿 边向点
边向点 以
以 的速度移动,点
的速度移动,点 从点
从点 开始沿
开始沿 边向点
边向点 以
以 的速度移动,当其中一点到达终点后,另外一点也随之停止运动.
的速度移动,当其中一点到达终点后,另外一点也随之停止运动.
 如果
如果 、
、 分别从
分别从 、
、 同时出发,那么几秒后,
同时出发,那么几秒后, 的面积等于
的面积等于 ?
? 在
在 中,
中, 的面积能否等于
的面积能否等于 ?请说明理由.
?请说明理由.
相关试题

