【题目】某商场经营某种品牌的玩具,进价是![]() 元,根据市场调查:在一段时间内,销售单价是
元,根据市场调查:在一段时间内,销售单价是![]() 元时,销售量是
元时,销售量是![]() 件,而销售单价每涨
件,而销售单价每涨![]() 元,就会少售出
元,就会少售出![]() 件玩具.
件玩具.
![]() 不妨设该种品牌玩具的销售单价为
不妨设该种品牌玩具的销售单价为![]() 元
元![]() ,请你分别用
,请你分别用![]() 的代数式来表示销售量
的代数式来表示销售量![]() 件和销售该品牌玩具获得利润
件和销售该品牌玩具获得利润![]() 元,并把结果填写在表格中:
元,并把结果填写在表格中:
销售单价(元) |
|
销售量 | ________ |
销售玩具获得利润 | ________ |
![]() 在
在![]() 问条件下,若商场获得了
问条件下,若商场获得了![]() 元销售利润,求该玩具销售单价
元销售利润,求该玩具销售单价![]() 应定为多少元.
应定为多少元.
![]() 在
在![]() 问条件下,若玩具厂规定该品牌玩具销售单价不低于
问条件下,若玩具厂规定该品牌玩具销售单价不低于![]() 元,且商场要完成不少于
元,且商场要完成不少于![]() 件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
参考答案:
【答案】(1)-10x+800,-10x2+1000x-16000;(2)该玩具销售单价x应定为60元;(3)商场销售该品牌服装获得的最大利润是8750元.
【解析】
(1)根据销售量与销售单价之间的变化关系就可以直接求出y与x之间的关系式;根据销售问题的利润=售价-进价就可以表示出w与x之间的关系;
(2)根据以上关于利润的相等关系列方程求解可得;
(3)根据销售单价不低于35元,销售量不少于350件建立不等式组求得x的范围,将函数解析式配方成顶点式,结合函数性质和x的范围求出其最大值即可.
(1)由题意,得:y=500-10(x-30)=-10x+800,
w=(-10x+800)(x-20)=-10x2+1000x-16000.
故答案为:-10x+800,-10x2+1000x-16000;
(2)根据题意,得:-10x2+1000x-16000=8000,
整理,得:x2-100x+2400=0,
解得:x=40或x=60,
∵x>40,
∴x=60,
答:该玩具销售单价x应定为60元;
(3)由题意知![]() ,
,
解得:35≤x≤45,
∵w=-10x2+1000x-16000=-10(x-50)2+9000,
∴当x<50时,w随x的增大而增大,
∴当x=45时,w取得最大值,最大值为-10(45-50)2+9000=8750,
答:商场销售该品牌服装获得的最大利润是8750元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
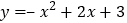 ,
, 画出二次函数
画出二次函数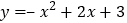 的图象,并根据图象说明,当
的图象,并根据图象说明,当 取何值时,图象位于
取何值时,图象位于 上方?
上方? 请说明经过怎样平移函数
请说明经过怎样平移函数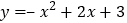 的图象得到函数
的图象得到函数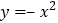 的图象.
的图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形
 的边长为
的边长为 ,将其放置在如图所示的平面直角坐标系中,其中
,将其放置在如图所示的平面直角坐标系中,其中 边在
边在 轴上,
轴上, 边的高
边的高 在
在 轴上.一只电子虫从
轴上.一只电子虫从 出发,先沿
出发,先沿 轴到达
轴到达 点,再沿
点,再沿 到达
到达 点,已知电子虫在
点,已知电子虫在 轴上运动的速度是在
轴上运动的速度是在 上运动速度的
上运动速度的 倍,若电子虫走完全程的时间最短,则点
倍,若电子虫走完全程的时间最短,则点 的坐标为________.
的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的方程
的方程
 若方程有两个有理数根,求整数
若方程有两个有理数根,求整数 的值
的值 若
若 满足不等式
满足不等式 ,试讨论方程根的情况.
,试讨论方程根的情况. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在
 中,
中, ,
, ,
, ,点
,点 从点
从点 开始沿
开始沿 边向点
边向点 以
以 的速度移动,点
的速度移动,点 从点
从点 开始沿
开始沿 边向点
边向点 以
以 的速度移动,当其中一点到达终点后,另外一点也随之停止运动.
的速度移动,当其中一点到达终点后,另外一点也随之停止运动.
 如果
如果 、
、 分别从
分别从 、
、 同时出发,那么几秒后,
同时出发,那么几秒后, 的面积等于
的面积等于 ?
? 在
在 中,
中, 的面积能否等于
的面积能否等于 ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为3的等边三角形,P是AB边上的一个动点,由A向B运动(P不与A、B重合),Q是BC延长线上一动点,与点P同时以相同的速度由C向BC延长线方向运动(Q不与C重合),

(1)当∠BPQ=90°时,求AP的长;
(2)过P作PE⊥AC于点E,连结PQ交AC于D,在点P、Q的运动过程中,线段DE的长是否发生变化?若不变,求出DE的长度;若变化,求出变化范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)如图1,△ABC是等腰锐角三角形,AB=AC(
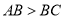 ),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;
),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;(2)如图2,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线;
(3)如图3,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数(如有需要,可在答题卡相应位置另外画图).

相关试题

