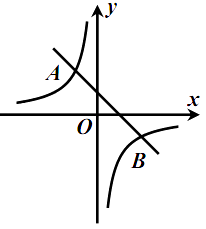
【题目】如图,一次函数 ![]() (
( ![]() )与反比例函数
)与反比例函数 ![]() (
( ![]() )的图象交于点
)的图象交于点 ![]() ,
, ![]() .
.
(1)求这两个函数的表达式;
(2)在 ![]() 轴上是否存在点
轴上是否存在点 ![]()
![]() ,使
,使 ![]() 为等腰三角形?若存在,求
为等腰三角形?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】
(1)
解:把A(-1,2)代入y=![]() ,得k2=-2,
,得k2=-2,
∴反比例函数的表达式为y=![]() 。
。
∵B(m,-1)在反比例函数的图象上,
∴m=2。
由题意得![]() ,解得
,解得![]()
∴一次函数的表达式为y=-x+1。
(2)
解:由A(-1,2)和B(2,-1),则AB=3![]()
①当PA=PB时,(n+1)2+4=(n-2)2+1,
∵n>0,∴n=0(不符合题意,舍去)
②当AP=AB时,22+(n+1)2=(3![]() )2
)2
∵n>0,∴n=-1+![]()
③当BP=BA时,12+(n-2)2=(3![]() )2
)2
∵n>0,∴n=2+![]()
所以n=-1+![]() 或n=2+
或n=2+![]() 。
。
【解析】(1)将点A代入反比例函数解析式可先求出k2,再求出点B的坐标,再运用待定系数法求k1和b的值;
(2)需要分类讨论,PA=PB,AP=AB,BP=BA,运用勾股定理求它们的长,构造方程求出n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副含
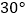 和
和 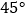 角的三角板
角的三角板 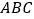 和
和 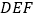 叠合在一起,边
叠合在一起,边 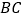 与
与 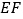 重合,
重合, 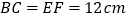 (如图1),点
(如图1),点 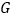 为边
为边 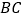
 的中点,边
的中点,边 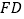 与
与 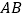 相交于点
相交于点  ,此时线段
,此时线段  的长是 . 现将三角板
的长是 . 现将三角板 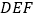 绕点
绕点 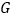 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 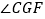 从
从 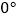 到
到 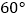 的变化过程中,点
的变化过程中,点  相应移动的路径长共为 . (结果保留根号)
相应移动的路径长共为 . (结果保留根号)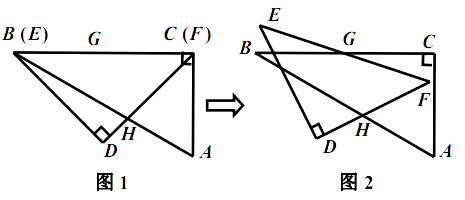
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=
 (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A. 6
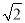 B. 10 C. 2
B. 10 C. 2 D. 2
D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
,  .
.
(1)在图中,用尺规作出 的内切圆
的内切圆  ,并标出
,并标出  与边
与边  ,
,  ,
,  的切点
的切点  ,
,  ,
,  (保留痕迹,不必写作法);
(保留痕迹,不必写作法);
(2)连接 ,
,  ,求
,求  的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与函数y=
 (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD= OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.(1)求m,k,n的值;
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明为了了解气温对用电量的影响,对去年自己家的每月用电量和当地气温进行了统计.当地去年每月的平均气温如图1,小明家去年月用电量如图2.
根据统计表,回答问题: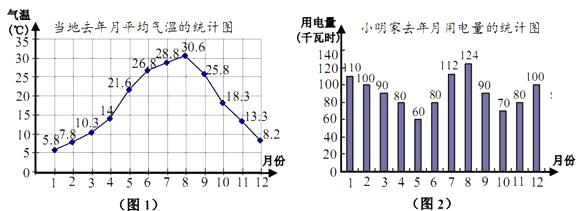
(1)当地去年月平均气温的最高值、最低值各为多少?相应月份的用电量各是多少?
(2)请简单描述月用电量与气温之间的关系;
(3)假设去年小明家用电量是所在社区家庭年用电量的中位数,据此他能否预测今年该社区的年用电量?请简要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形
 )靠墙摆放,高
)靠墙摆放,高  ,宽
,宽  ,小强身高
,小强身高  ,下半身
,下半身  ,洗漱时下半身与地面成
,洗漱时下半身与地面成  (
(  ),身体前倾成
),身体前倾成  (
(  ),脚与洗漱台距离
),脚与洗漱台距离  (点
(点  ,
,  ,
,  ,
,  在同一直线上).
在同一直线上).
(1)此时小强头部 点与地面
点与地面  相距多少?
相距多少?
(2)小强希望他的头部 恰好在洗漱盆
恰好在洗漱盆  的中点
的中点  的正上方,他应向前或后退多少?
的正上方,他应向前或后退多少?
( ,
,  ,
,  ,结果精确到
,结果精确到  )
)
相关试题

