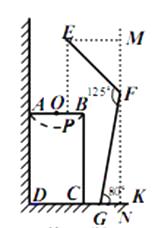
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形 ![]() )靠墙摆放,高
)靠墙摆放,高 ![]() ,宽
,宽 ![]() ,小强身高
,小强身高 ![]() ,下半身
,下半身 ![]() ,洗漱时下半身与地面成
,洗漱时下半身与地面成 ![]() (
( ![]() ),身体前倾成
),身体前倾成 ![]() (
( ![]() ),脚与洗漱台距离
),脚与洗漱台距离 ![]() (点
(点 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一直线上).
在同一直线上).
(1)此时小强头部 ![]() 点与地面
点与地面 ![]() 相距多少?
相距多少?
(2)小强希望他的头部 ![]() 恰好在洗漱盆
恰好在洗漱盆 ![]() 的中点
的中点 ![]() 的正上方,他应向前或后退多少?
的正上方,他应向前或后退多少?
( ![]() ,
, ![]() ,
, ![]() ,结果精确到
,结果精确到 ![]() )
)
参考答案:
【答案】
(1)
解:过点F作FN⊥DK于点N,过点E作EM⊥FN于点M,
∵EF+FG=166,FG=100,∴EF=66,
∵∠FGK=80°,∴FN=100sin80°≈98,
又∵∠EFG=125°,∴∠EFM=180°-125°-10°=45°,
∴FM=66cos45°=33![]() ≈46.53,
≈46.53,
∴MN=FN+FM≈144.5.
∴他头部E点与地面DK相距约144.5cm。
(2)
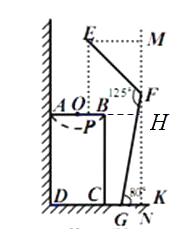
解:过点E作EP⊥AB于点P,延长OB交MN于点H。
∵AB=48,O为AB的中点,
∴AO=BO=24,
∵EM=66sin45°≈46.53,即PH≈46.53
GN=100cos80°≈1,8,CG=15,
∴OH=24+15+18==57
OP=OH-PH=57-46.53=10.47≈10.5,
∴他应向前10.5cm。
【解析】(1)过点F作FN⊥DK于点N,过点E作EM⊥FN于点M,他头部E点与地面DK的距离即为MN,由EF+FG=166,FG=100,则EF=66,由角的正弦值和余弦值即可解答;
(2)过点E作EP⊥AB于点P,延长OB交MN于点H,即求OP=OH-PH,而PH=EM,OH=OB+BH=OB+CG+GN,在Rt△EMF求出EM,在Rt△FGN求出GN即可.
【考点精析】认真审题,首先需要了解解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)).
-
科目: 来源: 题型:
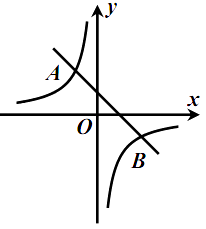
查看答案和解析>>【题目】如图,一次函数
 (
(  )与反比例函数
)与反比例函数  (
(  )的图象交于点
)的图象交于点  ,
,  .
.
(1)求这两个函数的表达式;
(2)在 轴上是否存在点
轴上是否存在点 
 ,使
,使  为等腰三角形?若存在,求
为等腰三角形?若存在,求  的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与函数y=
 (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD= OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.(1)求m,k,n的值;
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明为了了解气温对用电量的影响,对去年自己家的每月用电量和当地气温进行了统计.当地去年每月的平均气温如图1,小明家去年月用电量如图2.
根据统计表,回答问题: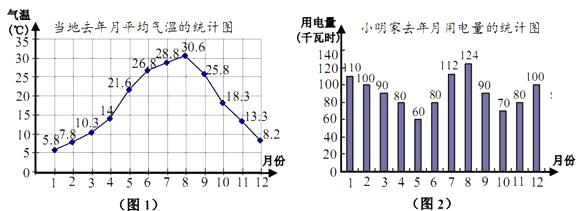
(1)当地去年月平均气温的最高值、最低值各为多少?相应月份的用电量各是多少?
(2)请简单描述月用电量与气温之间的关系;
(3)假设去年小明家用电量是所在社区家庭年用电量的中位数,据此他能否预测今年该社区的年用电量?请简要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
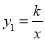 的图像与一次函数
的图像与一次函数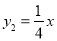 的图像交于点
的图像交于点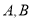 ,点
,点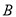 的横坐标是
的横坐标是4,点
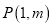 在反比例函数
在反比例函数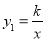 的图像上.
的图像上.(1)求反比例函数的表达式;
(2)观察图像回答:当
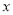 为何值时,
为何值时, 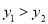 ;
;(3)求
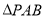 的面积.
的面积.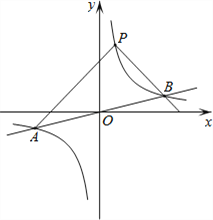
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是  的中线,
的中线, 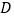 是线段
是线段  上一点(不与点
上一点(不与点  重合).
重合).  交
交  于点
于点  ,
,  ,连结
,连结 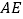 .
.
(1)如图1,当点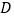 与
与  重合时,求证:四边形
重合时,求证:四边形  是平行四边形;
是平行四边形;
(2)如图2,当点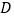 不与
不与  重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长 交
交  于点
于点  ,若
,若  ,且
,且  .
.
①求 的度数;
的度数;
②当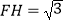 ,
,  时,求
时,求  的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日的钱塘江观潮信息如表:


按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离 (千米)与时间
(千米)与时间  (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点  ,点
,点 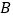 坐标为
坐标为  ,曲线
,曲线  可用二次函数
可用二次函数  (
(  ,
,  是常数)刻画.
是常数)刻画.
(1)求 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以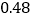 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为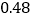 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度  ,
,  是加速前的速度).
是加速前的速度).
相关试题

