【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

参考答案:
【答案】(1)(﹣2,0);(2)①2;②(﹣3,5﹣t);③能确定, z=x+y.
【解析】试题分析:(1)根据平移的性质即可得到结论;
(2)①由点C的坐标为(-3,2).得到BC=3,CD=2,由于点P的横坐标与纵坐标互为相反数;于是确定点P在线段BC上,有PB=CD,即可得到结果;
②当点P在线段BC上时,点P的坐标(-t,2),当点P在线段CD上时,点P的坐标(-3,5-t);
③如图,过P作PE∥BC交AB于E,则PE∥AD,根据平行线的性质即可得到结论.
解:(1)根据题意,可得
三角形OAB沿x轴负方向平移3个单位得到三角形DEC,
∵点A的坐标是(1,0),
∴点E的坐标是(﹣2,0);
故答案为:(﹣2,0);
(2)①∵点C的坐标为(﹣3,2)
∴BC=3,CD=2,
∵点P的横坐标与纵坐标互为相反数;
∴点P在线段BC上,
∴PB=CD,
即t=2;
∴当t=2秒时,点P的横坐标与纵坐标互为相反数;
故答案为:2;
②当点P在线段BC上时,点P的坐标(﹣t,2),
当点P在线段CD上时,点P的坐标(﹣3,5﹣t);
③能确定,
如图,过P作PF∥BC交AB于F,
则FE∥AD,
∴∠1=∠CBP=x°,∠2=∠DAP=y°,
∴∠BPA=∠1+∠2=x°+y°=z°,
∴z=x+y.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)
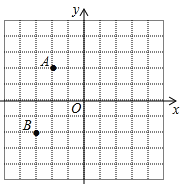
(1)若点D与点A关于y轴对称,则点D的坐标为 .
(2)将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为 .
(3)求A,B,C,D组成的四边形ABCD的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,
 的圆心坐标为
的圆心坐标为 ,半径为
,半径为 函数
函数 的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点. 连接CO,求证:
连接CO,求证:  ;
; 若
若 是等腰三角形,求点P的坐标;
是等腰三角形,求点P的坐标; 当直线PO与
当直线PO与 相切时,求
相切时,求 的度数;当直线PO与
的度数;当直线PO与 相交时,设交点为E、F,点M为线段EF的中点,令
相交时,设交点为E、F,点M为线段EF的中点,令 ,求s与t之间的函数关系,并写出t的取值范围.
,求s与t之间的函数关系,并写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1 , 四边形EFQP的面积为S2 , 四边形PQCB的面积为S3 .

(1)求证:EF+PQ=BC;
(2)若S1+S3=S2 , 求 的值;
的值;
(3)若S3﹣S1=S2 , 直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(
 )因式分解:
)因式分解:  ;
;(
 )计算:
)计算:  ;
;(
 )计算:
)计算:  ;
;(
 )解分式方程:
)解分式方程:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
,  ,
,  于
于 ,
,  于
于 .
.
求证:
 .
.证明:在
 和
和 中,
中,
∴
 ≌
≌ ( ).
( ).∴
 __________
__________ __________( ).
__________( ).∴
 是
是 的角平分线.
的角平分线.又∵
 于
于 ,
,  于
于 ,
,∴
 ( ).
( ). -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A.y=3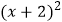 +3
+3
B.y=3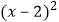 +3
+3
C.y=3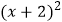 -3
-3
D.y=3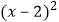 -3
-3
相关试题

