【题目】对于一元二次方程ax2+bx+c=0 (a≠0),下列说法中错误的是( )
A. 当a>0,c<0时,方程一定有实数根
B. 当c=0时,方程至少有一个根为0
C. 当a>0,b=0,c<0时,方程的两根一定互为相反数
D. 当abc<0时,方程的两个根同号,当abc>0时,方程的两个根异号
参考答案:
【答案】D
【解析】解:A.正确.当a>0,c<0时,△=b2﹣4ac>0,则方程一定有实数根;
B.正确.当c=0时,则ax2+bx=0,则方程至少有一个根为0;
C.正确.当a>0,b=0,c<0时,方程两根为x1,x2,x1+x2=![]() =0,则方程的两根一定互为相反数;
=0,则方程的两根一定互为相反数;
D.错误.当ac<0时,方程的两个根异号,当ac>0时,方程的两个根同号.
故选D.
-
科目: 来源: 题型:
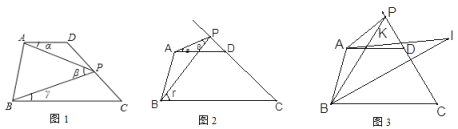
查看答案和解析>>【题目】如图,已知四边形ABCD,AD∥BC.点P在直线CD上运动(点P和点C,D不重合,点P,A,B不在同一条直线上),若记∠DAP,∠APB,∠PBC分别为∠α,∠β,∠γ.
(1)如图1,当点P在线段CD上运动时,写出∠α,∠β,∠γ之间的关系并说出理由;
(2)如图2,如果点P在线段CD的延长线上运动,探究∠α,∠β,∠γ之间的关系,并说明理由.
(3)如图3,BI平分∠PBC,AI交BI于点I,交BP于点K,且∠PAI:∠DAI=5:1,∠APB=20°,∠I=30°,求∠PAI的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 中,过B点作BE⊥AD,
中,过B点作BE⊥AD, .
.(1)如图1,点
 在
在 的延长线上,连
的延长线上,连 ,作
,作 于
于 ,交
,交 于点
于点 .求证:
.求证: ;
;(2)如图2,点
 在线段
在线段 上,连
上,连 ,过
,过 作
作 ,且
,且 ,连
,连 交
交 于
于 ,连
,连 ,问
,问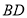 与
与 有何数量关系,并加以证明;
有何数量关系,并加以证明;(3)如图3,点
 在CB延长线上,
在CB延长线上, 且
且 ,连接
,连接 、
、 的延长线交
的延长线交 于点
于点 ,若
,若 ,请直接写出
,请直接写出 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
,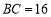 ,点
,点 从点
从点 出发向点
出发向点 运动,运动到点
运动,运动到点 停止,同时,点
停止,同时,点 从点
从点 出发向点
出发向点 运动,运动到点
运动,运动到点 即停止,点
即停止,点 、
、 的速度都是每秒1个单位,连接
的速度都是每秒1个单位,连接 、
、 、
、 .设点
.设点 、
、 运动的时间为
运动的时间为 秒
秒(1)当
 为何值时,四边形
为何值时,四边形 是矩形;
是矩形;(2)当
 时,判断四边形
时,判断四边形 的形状,并说明理由;
的形状,并说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
 根据图示填写下表:
根据图示填写下表:平均数
 分
分中位数
 分
分众数
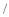 分
分A校
______
85
______
B校
85
______
100
 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好; 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:求代数式x2+4x+8的最小值.
解:因为x2+4x+8=(x2+4x+4)+4=(x+2)2+4≥4,所以当x=﹣2时,代数式x2+4x+8有最小值,最小值是4.仿照上述解题过程求值.
(1)应用:求代数式m2+2m+3的最小值.
(2)拓展:求代数式﹣m2+3m+
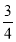 的最大值.
的最大值.
相关试题

