【题目】阅读理解:求代数式x2+4x+8的最小值.
解:因为x2+4x+8=(x2+4x+4)+4=(x+2)2+4≥4,所以当x=﹣2时,代数式x2+4x+8有最小值,最小值是4.仿照上述解题过程求值.
(1)应用:求代数式m2+2m+3的最小值.
(2)拓展:求代数式﹣m2+3m+![]() 的最大值.
的最大值.
参考答案:
【答案】(1)2;(2)-![]() .
.
【解析】
(1)利用配方法,仿照上面的例子将代数式配方,求最小值即可,
(2)利用配方法,仿照上面的例子将代数式配方,求最大值即可.
(1)m2+2m+3=(m2+2m+1)+2=(m+1)2+2≥2,
所以当m=﹣1时,代数式m2+2m+3有最小值,最小值是2,
(2)﹣m2+3m+![]() =﹣(m2﹣3m+
=﹣(m2﹣3m+![]() )﹣
)﹣![]() +
+![]() =﹣(m-
=﹣(m-![]() )2﹣
)2﹣![]() ≤﹣
≤﹣![]() ,
,
所以当m=![]() 时,代数式﹣m2+3m+
时,代数式﹣m2+3m+![]() 有最大值,最大值是﹣
有最大值,最大值是﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一元二次方程ax2+bx+c=0 (a≠0),下列说法中错误的是( )
A. 当a>0,c<0时,方程一定有实数根
B. 当c=0时,方程至少有一个根为0
C. 当a>0,b=0,c<0时,方程的两根一定互为相反数
D. 当abc<0时,方程的两个根同号,当abc>0时,方程的两个根异号
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
,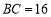 ,点
,点 从点
从点 出发向点
出发向点 运动,运动到点
运动,运动到点 停止,同时,点
停止,同时,点 从点
从点 出发向点
出发向点 运动,运动到点
运动,运动到点 即停止,点
即停止,点 、
、 的速度都是每秒1个单位,连接
的速度都是每秒1个单位,连接 、
、 、
、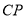 .设点
.设点 、
、 运动的时间为
运动的时间为 秒
秒(1)当
 为何值时,四边形
为何值时,四边形 是矩形;
是矩形;(2)当
 时,判断四边形
时,判断四边形 的形状,并说明理由;
的形状,并说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
 根据图示填写下表:
根据图示填写下表:平均数
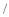 分
分中位数
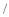 分
分众数
 分
分A校
______
85
______
B校
85
______
100
 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好; 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为C(a,0),点C的坐标为(0,b),且a,b满足(a﹣4)2+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→C→B→A→O的路线移动.
(1)a= ,b= ,点B的坐标为 .
(2)当点P移动4秒时,请说明点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为
 ,所以这个三角形是常态三角形.
,所以这个三角形是常态三角形.(1)若
 三边长分别是2,
三边长分别是2, 和4,则此三角形 常态三角形(填“是”或“不是”
和4,则此三角形 常态三角形(填“是”或“不是”  ;
;(2)如图,
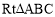 中,
中, ,
, ,点
,点 为
为 的中点,连接
的中点,连接 ,若
,若 是常态三角形,求
是常态三角形,求 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
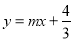 的图象为直线
的图象为直线 ,函数
,函数 的图象为直线
的图象为直线 ,直线
,直线 、
、 分别交
分别交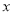 轴于点
轴于点 和点
和点 ,分别交
,分别交 轴于点
轴于点 和
和 ,
, 和
和 相交于点
相交于点
(1)填空:
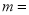 ;求直线
;求直线 的解析式为 ;
的解析式为 ;(2)若点
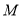 是
是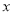 轴上一点,连接
轴上一点,连接 ,当
,当 的面积是
的面积是 面积的2倍时,请求出符合条件的点
面积的2倍时,请求出符合条件的点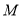 的坐标;
的坐标;(3)若函数
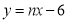 的图象是直线
的图象是直线 ,且
,且 、
、 、
、 不能围成三角形,直接写出
不能围成三角形,直接写出 的值.
的值.
相关试题

