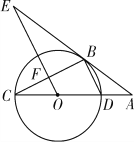
【题目】如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.
(1)求证:∠E=∠C;
(2)若⊙O的半径为3,AD=2,试求AE的长;
(3)求△ABC的面积.
参考答案:
【答案】(1)证明见解析;(2)10;(3)![]()
【解析】试题分析:(1)连接OB,利用已知条件和切线的性质证明:OE∥BD,即可证明:∠E=∠C;
(2)根据题意求出AB的长,然后根据平行线分线段定理,可求解;
(3)根据相似三角形的面积比等于相似比的平方可求解.
试题解析:(1)如解图,连接OB,
∵CD为⊙O的直径,
∴∠CBD=∠CBO+∠OBD=90°,
∵AB是⊙O的切线,
∴∠ABO=∠ABD+∠OBD=90°,
∴∠ABD=∠CBO.
∵OB、OC是⊙O的半径,
∴OB=OC,∴∠C=∠CBO.
∵OE∥BD,∴∠E=∠ABD,
∴∠E=∠C;
(2)∵⊙O的半径为3,AD=2,
∴AO=5,∴AB=4.
∵BD∥OE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BE=6,AE=6+4=10
(3)S△AOE=![]()
![]() =15,然后根据相似三角形面积比等于相似比的平方可得
=15,然后根据相似三角形面积比等于相似比的平方可得
S△ABC= ![]() S△AOE=
S△AOE=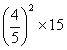 =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年中考,池州市市贵池区区计划在4月中旬的某个周二至周四这3天进行理化加试.王老师和朱老师都将被邀请当监考老师,王老师随机选择2天,朱老师随机选择1天当监考老师.
(1)求王老师选择周二、周三这两天的概率是多少?
(2)求王老师和朱老师两人同一天监考理化加试的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算,正确的是( )
A.x4﹣x3=x
B.x6÷x3=x2
C.xx3=x4
D.(xy3)2=xy6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如表记录了一名球员在罚球线上投篮的结果.那么,这名球员投篮一次,投中的概率约为(精确到0.1).
投篮次数(n)
50
100
150
200
250
300
500
投中次数(m)
28
60
78
104
123
152
251
投中频率(m/n)
0.56
0.60
0.52
0.52
0.49
0.51
0.50
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是正方形
是正方形 内一点,连接
内一点,连接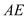 、
、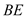 、
、 ,并延长
,并延长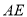 与
与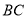 交于点
交于点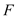 ,
, 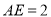 ,
, 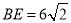 ,
,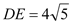 ,将
,将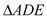 绕点
绕点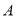 旋转至
旋转至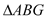 ,连接
,连接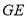 、
、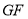 ,则线段
,则线段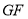 的长为___________.
的长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学某年级为了选拔参加“全国汉字听写大赛”重庆赛区比赛的队员,特在年级举行全体学生的“汉字听写”比赛,首轮每位学生听写汉字39个.现随机抽取了部分学生的听写结果,绘制成如下的图表.

根据以上信息完成下列问题:
(1)统计表中的
 = ,
= ,  = ,并补全条形统计图;
= ,并补全条形统计图;(2)第二轮比赛过后,为了更有针对性地应对本次大赛,该年级决定从没有担任班主任的3名语文教师(其中1名男教师2名女教师)中随机抽取两名教师对胜出的学生进行培训、辅导.请用树状图或列表法求出抽取的两名教师恰好都是女教师的概率.
-
科目: 来源: 题型:
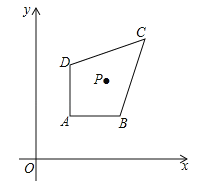
查看答案和解析>>【题目】如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n﹣m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n﹣m的值.
相关试题

