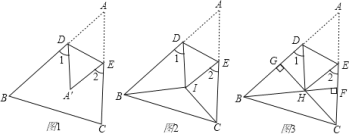
【题目】(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,若∠A=50°,求∠1+∠2的度数,猜想并直接写出∠1+∠2与∠A的数量关系.(不必证明)
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=110°,求∠BIC的度数;
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
参考答案:
【答案】(1)100°,∠1+∠2=2∠A;(2)117.5°;(3)∠BHC=180°-![]() (∠1+∠2),证明见解析.
(∠1+∠2),证明见解析.
【解析】
(1)根据翻折变换的性质以及三角形内角和定理以及平角的定义求出即可;
(2)根据三角形角平分线的性质得出∠IBC+∠ICB=90°-![]() ∠A,得出∠BIC的度数即可;
∠A,得出∠BIC的度数即可;
(3)根据翻折变换的性质以及垂线的性质得出,∠AFH+∠AGH=90°+90°=180°,进而求出∠A=![]() (∠1+∠2),即可得出答案.
(∠1+∠2),即可得出答案.
(1)∠1+∠2=2∠A;
理由:根据翻折的性质,∠ADE=![]() (180°-∠1),∠AED=
(180°-∠1),∠AED=![]() (180°-∠2),
(180°-∠2),
∵∠A+∠ADE+∠AED=180°,
∴∠A+![]() (180-∠1)+
(180-∠1)+![]() (180-∠2)=180°,
(180-∠2)=180°,
整理得2∠A=∠1+∠2,
∵∠A=50°,
∴∠1+∠2=100°,
猜想:∠1+∠2=2∠A;
(2)由(1)∠1+∠2=2∠A,得2∠A=110°,∴∠A=55°,
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A,
∠A,
∴∠BIC=180°-(∠IBC+∠ICB)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ×55°=117.5°;
×55°=117.5°;
(3)∵BF⊥AC,CG⊥AB,
∴∠AFH+∠AGH=90°+90°=180°,
∴∠FHG+∠A=360°-180°=180°,
∴∠BHC=∠FHG=180°-∠A,
由(1)知∠1+∠2=2∠A,
∴∠A=![]() (∠1+∠2),
(∠1+∠2),
∴∠BHC=180°-![]() (∠1+∠2).
(∠1+∠2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE. 求证:四边形BCDE是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
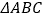 的
的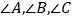 所对边分别是
所对边分别是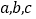 ,且
,且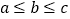 ,若满足
,若满足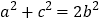 ,则称
,则称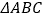 为奇异三角形,例如等边三角形就是奇异三角形.
为奇异三角形,例如等边三角形就是奇异三角形.(1)若
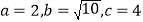 ,判断
,判断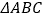 是否为奇异三角形,并说明理由;
是否为奇异三角形,并说明理由;(2)若
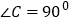 ,
,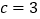 ,求
,求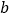 的长;
的长;(3)如图2,在奇异三角形
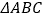 中,
中,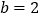 ,点
,点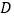 是
是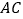 边上的中点,连结
边上的中点,连结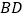 ,
,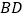 将
将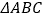 分割成2个三角形,其中
分割成2个三角形,其中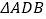 是奇异三角形,
是奇异三角形,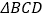 是以
是以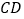 为底的等腰三角形,求
为底的等腰三角形,求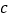 的长.
的长.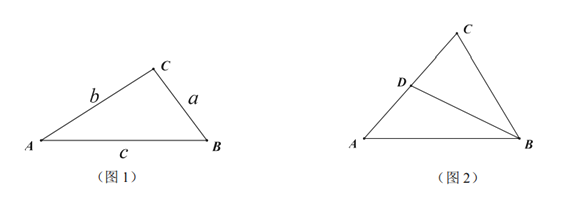
-
科目: 来源: 题型:
查看答案和解析>>【题目】课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,
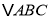 中,若
中,若 ,
,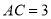 ,求
,求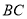 边上的中线
边上的中线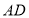 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将
的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将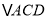 绕点
绕点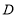 逆时针旋转
逆时针旋转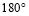 得到
得到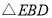 ,把
,把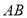 、
、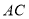 、
、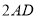 集中在
集中在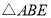 中,利用三角形的三边关系可得
中,利用三角形的三边关系可得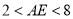 ,则
,则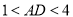 ;
;(2)问题解决:受到(1)的启发,请你证明下面命题:如图2,在
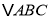 中,
中,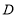 是
是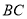 边上的中点,
边上的中点,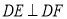 ,
,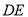 交
交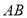 于点
于点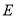 ,
,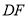 交
交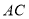 于点
于点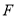 ,连接
,连接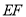 .
.①求证:
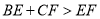 ;
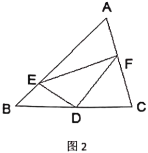
;②如图3,若
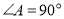 ,探索线段
,探索线段 、
、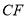 、
、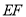 之间的等量关系,并加以证明.
之间的等量关系,并加以证明.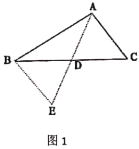
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE.

(1)求证:AE=BD;
(2)求证:四边形ADCE是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )

A.AB=CDB.AB∥CDC.∠A=∠CD.BC=AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形中的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,……,按此规律第5个图中共有点的个数是( )

A. 31 B. 46 C. 51 D. 66
相关试题

