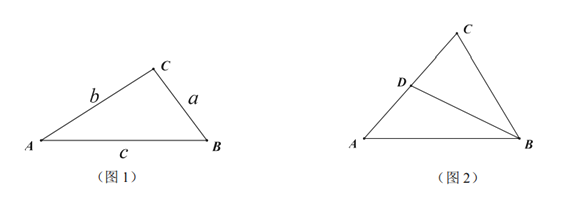
【题目】如图1,![]() 的
的![]() 所对边分别是
所对边分别是![]() ,且
,且![]() ,若满足
,若满足![]() ,则称
,则称![]() 为奇异三角形,例如等边三角形就是奇异三角形.
为奇异三角形,例如等边三角形就是奇异三角形.
(1)若![]() ,判断
,判断![]() 是否为奇异三角形,并说明理由;
是否为奇异三角形,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图2,在奇异三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,连结
边上的中点,连结![]() ,
,![]() 将
将![]() 分割成2个三角形,其中
分割成2个三角形,其中![]() 是奇异三角形,
是奇异三角形,![]() 是以
是以![]() 为底的等腰三角形,求
为底的等腰三角形,求![]() 的长.
的长.
参考答案:
【答案】(1)是,理由见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据奇异三角形的概念直接进行判断即可.
(2)根据勾股定理以及奇异三角形的概念直接列式进行计算即可.
(3)根据△ABC是奇异三角形,且b=2,得到![]() ,由题知:AD=CD=1,且BC=BD=a,根据△ADB是奇异三角形,则
,由题知:AD=CD=1,且BC=BD=a,根据△ADB是奇异三角形,则![]() 或
或![]() ,分别求解即可.
,分别求解即可.
(1)∵![]() ,
, ![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
即△ABC是奇异三角形.
(2)∵∠C=90°,![]()
∴![]()
∵![]()
∴![]()
![]() ,
,
∴![]()
解得:![]() .
.
(3)∵△ABC是奇异三角形,且b=2
∴![]()
由题知:AD=CD=1,BC=BD=a
∵△ADB是奇异三角形,且![]() ,
,![]()
∴![]() 或
或![]()
当![]() 时,
时,![]() 时,与
时,与![]() 矛盾,不合题意.
矛盾,不合题意.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某开发公司生产的 960 件新产品需要精加工后,才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用 20 天,而甲工厂每天加工的数量是乙工厂每天加工的数量的
 ,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家合作完成.在加工过程中,公司派一名工程师每天到厂进行技术指导,并负担每天 15 元的午餐补助费, 请你帮公司选择一种既省时又省钱的加工方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证:
(1)四边形AFBE是矩形;
(2)MN= BC.
BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE. 求证:四边形BCDE是矩形.

-
科目: 来源: 题型:
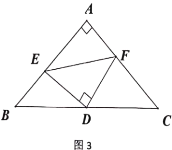
查看答案和解析>>【题目】课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,
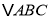 中,若
中,若 ,
, ,求
,求 边上的中线
边上的中线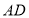 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将
的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将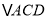 绕点
绕点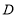 逆时针旋转
逆时针旋转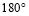 得到
得到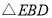 ,把
,把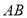 、
、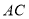 、
、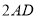 集中在
集中在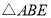 中,利用三角形的三边关系可得
中,利用三角形的三边关系可得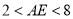 ,则
,则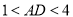 ;
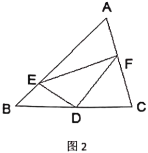
;(2)问题解决:受到(1)的启发,请你证明下面命题:如图2,在
 中,
中,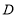 是
是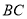 边上的中点,
边上的中点,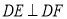 ,
,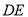 交
交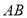 于点
于点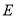 ,
,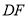 交
交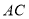 于点
于点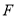 ,连接
,连接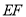 .
.①求证:
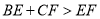 ;
;②如图3,若
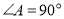 ,探索线段
,探索线段 、
、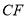 、
、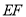 之间的等量关系,并加以证明.
之间的等量关系,并加以证明.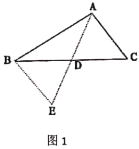
-
科目: 来源: 题型:
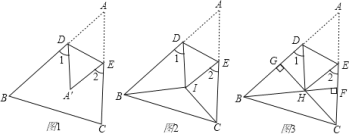
查看答案和解析>>【题目】(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,若∠A=50°,求∠1+∠2的度数,猜想并直接写出∠1+∠2与∠A的数量关系.(不必证明)
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=110°,求∠BIC的度数;
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE.

(1)求证:AE=BD;
(2)求证:四边形ADCE是矩形.
相关试题

