Question

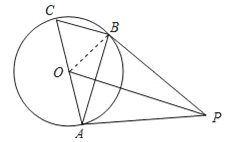
【题目】如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PA，PB，AB，已知∠PBA=∠C．

（1）求证：PB是⊙O的切线；

（2）连接OP，若OP∥BC，且OP=8，⊙O的半径为，求BC的长．

Answer 1

【答案】（1）详见解析；（2）BC=2．

【解析】试题分析：（1）连接OB，由圆周角定理得出∠ABC=90°，得出∠C+∠BAC=90°，再由OA=OB，得出∠BAC=∠OBA，证出∠PBA+∠OBA=90°，即可得出结论；

（2）证明△ABC∽△PBO，得出对应边成比例，即可求出BC的长．

试题解析：（1）证明：连接OB，如图所示：

∵AC是⊙O的直径，

∴∠ABC=90°，

∴∠C+∠BAC=90°，

∵OA=OB，

∴∠BAC=∠OBA，

∵∠PBA=∠C，

∴∠PBA+∠OBA=90°，

即PB⊥OB，

∴PB是⊙O的切线；

（2）解：∵⊙O的半径为2，

∴OB=2，AC=4，

∵OP∥BC，

∴∠C=∠BOP，

又∵∠ABC=∠PBO=90°，

∴△ABC∽△PBO，

∴，

即，

∴BC=2．