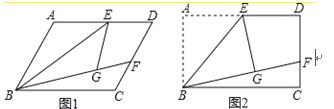
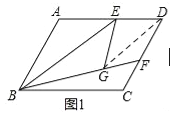
【题目】如图1,ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且 点G在□ABCD内部.将BG延长交DC于点F.
(1)猜想并填空:GF DF(填“>”、“<”、“=”);
(2)请证明你的猜想;
(3)如图2,当∠A=90°,设BG=a,GF=b,EG=c,证明:c2=ab.
参考答案:
【答案】(1)=;(2)证明见解析;(3)证明见解析.
【解析】(1)GF=DF,
故答案为:=;
(2)理由是:
连接DG,
由折叠得:AE=EG,∠A=∠BGE,
∵E在AD的中点,
∴AE=ED,
∴ED=EG,
∵∠EGD=∠EDG,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A+∠ADC=180°,
∵∠BGE+∠EGF=180°,
∴∠EDF=∠EGF,
∴∠EDF﹣∠EDG=∠EGF﹣∠EGD,
即∠GDF=∠DGF,
∴GF=DF;
(3)证明:如题图2,由(2)得:DF=GF=b,
由图可得:BF=BG+GF=a+b,
由折叠可得:AB=BG=a,AE=EG=c,
在平行四边形ABCD中,
BC=AD=2AE=2c,CD=AB=a,
∴CF=CD﹣DF=a﹣b,
∵∠A=90°,
∴□ABCD是矩形,
∴∠C=90°,
在Rt△BCF中,由勾股定理得,
BC2+CF2=BF2,
∴(2c)2+(a﹣b)2=(a+b)2,
整理得:c2=ab.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.
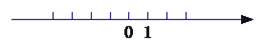
(1)若1表示的点与-1表示的点重合,则-2表示的点与数 表示的点重合;
(2)若-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
② 若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆O的半径为3cm,点P是直线l上的一点,且OP=3cm,则直线l与圆O的位置关系为( )
A. 相切 B. 相交 C. 相离 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州市成功申办2022年亚运会,这将推动杭州市体育事业发展,为了促进全民健身活动的发展,某社区为辖区内学校购买一批篮球和足球,已知篮球和足球的单价分别为120元和90元.
(1)根据实际需要,社区决定购买篮球和足球共100个,其中篮球购买的数量不少于40个,社区可用于购买这批篮球和足球的资金最多为10260元,请问有几种购买方案;
(2)若购买篮球
 个,学校购买这批篮球和足球的总费用为
个,学校购买这批篮球和足球的总费用为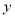 元,在(1)的条件下,求哪种方案能使
元,在(1)的条件下,求哪种方案能使 最小,并求出
最小,并求出 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中共装有红球、黄球和蓝球320个,这些球除颜色外都相同.小明每次从中任意摸出一个球,记下颜色后将球放回并搅匀,通过多次重复试验,算得摸到红球的频率是25 %,则估计这只袋子中有红球________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2+x﹣2与x2+3x+2的公因式是( )
A.x+1B.x﹣1C.x+2D.x﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(3,4)先向左平移5个单位,再向下平移2个单位得到点B,则点B的坐标为 .
相关试题

