【题目】已知抛物线y=x2+bx+c与x轴交于点A(-2,0).
(1)填空:c= (用含b的式子表示)。
(2)若b<4
①求证:抛物线与x轴有两个交点;
②设抛物线与x轴的另一个交点为B,当线段AB上恰有5个整点(横坐标、纵坐标都是整数的点),直接写出b的取值范围为 ;
(3)直线y=x-4经过抛物线y=x2+bx+c的顶点P,求抛物线的表达式。
参考答案:
【答案】(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]() ;(3)
;(3)![]() 或
或![]()
【解析】试题分析:
(1)把点A(-2,0)代入y=x2+bx+c中得到关于b、c的等式,将等式变形即可得到用含“b”表示的c;
(2)①由(1)中所得结果可得:△=![]() ,结合b<4可得△>0,由此即可得到抛物线和x轴有两个不同的交点;
,结合b<4可得△>0,由此即可得到抛物线和x轴有两个不同的交点;
②根据①中所得结果可表达出抛物线与x轴的另一个交点B的坐标为![]() ,结合线段AB上恰好有5个整数点,即可求得b的取值范围;
,结合线段AB上恰好有5个整数点,即可求得b的取值范围;
(3)将抛物线![]() 配方,得到用“b”表达的顶点P的坐标,将所得坐标代入
配方,得到用“b”表达的顶点P的坐标,将所得坐标代入![]() 解出b的值,再代回
解出b的值,再代回![]() 中即可求得二次函数的解析式.
中即可求得二次函数的解析式.
试题解析:
(1)把点A(-2,0)代入y=x2+bx+c得: ![]() ,
,
∴c=2b-4;
(2)① ∵在![]() 中,
中, ![]() ,
,
∴当![]() 时,
时, ![]() ,
,
即 ![]() ,
,
∴当![]() 时,抛物线与x轴有两个交点;
时,抛物线与x轴有两个交点;
②当![]() 时,有
时,有![]() ,
,
∵当![]() 时,
时, ![]() ,
,
∴ ,
,
∴![]() ,
,
∴点B的坐标为![]() ,
,
当点B在点A的右边时,
∵点A的坐标为(-2,0),且线段AB上恰好有5个知识点,
∴这5个整数点所对应的数分别是-2,-1,0,1,2,
∴![]() ,
,
∴此时b的取值范围是: ![]() ;
;
当点B在点A的左侧时,这5个整数点分别是:-2,-3,-4,-5,-6,
∴![]() ,即
,即![]() ,解得:
,解得: ![]() ,
,
∵b<4,
∴此种情况不成立;
综上所述,可得b的取值范围为: ![]() ;
;
(3)∵![]()
∴顶点P的坐标为:  ,
,
将其代入![]() 中,得,
中,得, ![]() ,
,
解得, ![]() ,
,
∴抛物线的表达式为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中点A的坐标为(0,6),点B的坐标为(﹣
 ,5),将△AOB沿x轴向左平移得到△A′O′B′,点A的对应点A′落在直线y=﹣
,5),将△AOB沿x轴向左平移得到△A′O′B′,点A的对应点A′落在直线y=﹣ x上,则点B的对应点B′的坐标为( )
x上,则点B的对应点B′的坐标为( )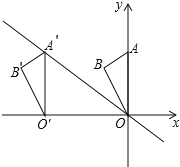
A.(﹣8,6)B.(﹣
 ,5)C.(﹣
,5)C.(﹣ ,5)D.(﹣8,5)
,5)D.(﹣8,5) -
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车租赁公司要购买轿车和面包车共
 辆.其中面包车不能超过轿车的两倍,轿车每辆
辆.其中面包车不能超过轿车的两倍,轿车每辆 万元,面包车每辆
万元,面包车每辆 万元,公司可投入的购车款不超过61万元.
万元,公司可投入的购车款不超过61万元.(小题1)符合公司要求的购买方案有哪几种?请说明理由.
(小题2)如果每辆轿车的日租金为
 元,每辆面包车的日租金为
元,每辆面包车的日租金为 元.假设新购买的这
元.假设新购买的这 辆车每日都可租出,要使这
辆车每日都可租出,要使这 辆车的日租金收入不低于1600元,那么应选择以上哪种购买方案?
辆车的日租金收入不低于1600元,那么应选择以上哪种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=3
 ,BC=10,∠A=45°,点E是边AD上一动点,将△AEB沿直线BE折叠,得到△FEB,设BF与AD交于点M,当BF与ABCD的一边垂直时,DM的长为_____.
,BC=10,∠A=45°,点E是边AD上一动点,将△AEB沿直线BE折叠,得到△FEB,设BF与AD交于点M,当BF与ABCD的一边垂直时,DM的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校七年级男生的体能情况,体育老师随即抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2尚不完整的统计图.
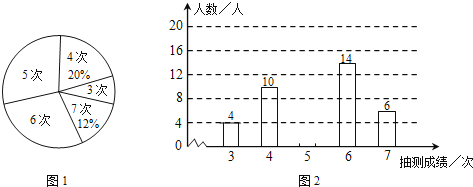
(1)本次抽测的男生有多少人,
(2)请你将图2的统计图补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校350名七年级男生中,估计有多少人体能达标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线。
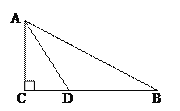
(1)以AB上一点O为圆心,AD为弦作⊙O;
(2)求证:BC为⊙O的切线;
(3)如果AC=3,tanB=
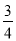 ,求⊙O的半径。
,求⊙O的半径。 -
科目: 来源: 题型:
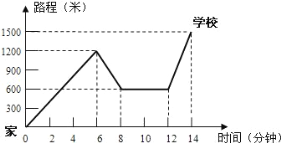
查看答案和解析>>【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
相关试题

