搜索
【题目】如图，在平面直角坐标系中点A的坐标为(0，6)，点B的坐标为(﹣
，5)，将△AOB沿x轴向左平移得到△A′O′B′，点A的对应点A′落在直线y＝﹣
x上，则点B的对应点B′的坐标为（ ）
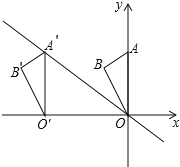
A.(﹣8，6)B.(﹣
，5)C.(﹣
，5)D.(﹣8，5)
参考答案：
【答案】C
【解析】
根据题意确定点A′的纵坐标，根据点A′落在直线y＝﹣
x上，求出点A′的横坐标，确定△OAB沿x轴向左平移的单位长度即可得到答案．
解：由题意可知，点A移动到点A′位置时，纵坐标不变，
∴点A′的纵坐标为6，
∵点A′落在直线上y＝﹣x上，
∴﹣x＝6，解得x＝﹣8，
∴△OAB沿x轴向左平移得到△O′A′B′位置，移动了8个单位，
∴点B与其对应点B′的坐标为（﹣
，5），
故答案选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中的位置如图所示．将△ABC向右平移6个单位长度，再向下平移6个单位长度得到△A1B1C1．(图中每个小方格边长均为1个单位长度)．
（1）在图中画出平移后的△A1B1C1；
（2）直接写出△A1B1C1各顶点的坐标
（3）求出△A1B1C1的面积
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD、BC垂直相交于点O，AB∥CD，又BC = 8，AD = 6，求：AB＋CD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各曲线中不能表示y是x的函数是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某汽车租赁公司要购买轿车和面包车共
辆．其中面包车不能超过轿车的两倍，轿车每辆
万元，面包车每辆
万元，公司可投入的购车款不超过61万元．（小题1）符合公司要求的购买方案有哪几种？请说明理由．
（小题2）如果每辆轿车的日租金为
元，每辆面包车的日租金为
元．假设新购买的这辆车每日都可租出，要使这辆车的日租金收入不低于1600元，那么应选择以上哪种购买方案？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，AB＝3
，BC＝10，∠A＝45°，点E是边AD上一动点，将△AEB沿直线BE折叠，得到△FEB，设BF与AD交于点M，当BF与ABCD的一边垂直时，DM的长为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=x2+bx+c与x轴交于点A(－2,0).
(1)填空：c= (用含b的式子表示)。
(2)若b＜4
①求证：抛物线与x轴有两个交点；
②设抛物线与x轴的另一个交点为B，当线段AB上恰有5个整点（横坐标、纵坐标都是整数的点），直接写出b的取值范围为 ；
(3)直线y=x－4经过抛物线y=x2+bx+c的顶点P，求抛物线的表达式。
相关试题
