【题目】如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线。
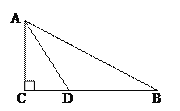
(1)以AB上一点O为圆心,AD为弦作⊙O;
(2)求证:BC为⊙O的切线;
(3)如果AC=3,tanB=![]() ,求⊙O的半径。
,求⊙O的半径。
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:
(1)由题意可知,作线段AD的垂直平分线与AB相交,交点即为圆心O,然后以O为圆心OA为半径作圆即可;
(2)连接OD,由已知易证∠ODA=∠OAD=∠CAD,从而可得OD∥AC,由此可得∠ODB=∠C=90°,结合OD是⊙O的半径即可得到BC和⊙O相切;
(3)由已知条件易得BC=4和AB=5的长度,设⊙O的半径为r,则OD=OA=r,OB=5-r;由OD∥AC可得△BDO∽△BCA,这样由相似三角形对应边成比例即可列出关于r的方程,解方程即可求得r的值.
试题解析:
(1)如图所示,⊙O为所求圆;
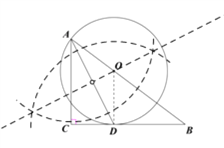
(2)连接OD.
∵AD平分∠CAB
∴∠CAD=∠BAD
又∵OA=OD
∴∠OAD=∠ODA
∴∠CAD=∠ODA
∴OD∥AC
∴∠ODB=∠C=90°
又∵OD为半径
∴BC是⊙O的切线.
(3)∵在△ABC中,AC=3,tanB=![]() ,∠C=90°,
,∠C=90°,
∴BC=4,AB=5,
设⊙O的半径为r,则OA=OD=r,BO=5-r
∵OD∥AC
∴△BOD∽△BAC
∴![]()
即 ![]()
解得, ![]() ,
,
∴⊙O的半径为 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=3
 ,BC=10,∠A=45°,点E是边AD上一动点,将△AEB沿直线BE折叠,得到△FEB,设BF与AD交于点M,当BF与ABCD的一边垂直时,DM的长为_____.
,BC=10,∠A=45°,点E是边AD上一动点,将△AEB沿直线BE折叠,得到△FEB,设BF与AD交于点M,当BF与ABCD的一边垂直时,DM的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+bx+c与x轴交于点A(-2,0).
(1)填空:c= (用含b的式子表示)。
(2)若b<4
①求证:抛物线与x轴有两个交点;
②设抛物线与x轴的另一个交点为B,当线段AB上恰有5个整点(横坐标、纵坐标都是整数的点),直接写出b的取值范围为 ;
(3)直线y=x-4经过抛物线y=x2+bx+c的顶点P,求抛物线的表达式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校七年级男生的体能情况,体育老师随即抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2尚不完整的统计图.
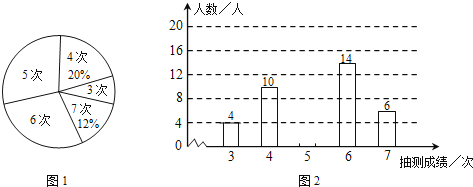
(1)本次抽测的男生有多少人,
(2)请你将图2的统计图补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校350名七年级男生中,估计有多少人体能达标?
-
科目: 来源: 题型:
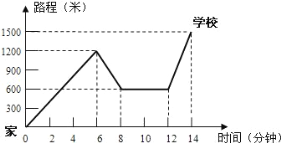
查看答案和解析>>【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
-
科目: 来源: 题型:
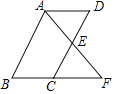
查看答案和解析>>【题目】如图,点E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若AB=8,BC=5,则EF的长为 时,AB⊥AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
相关试题

