【题目】把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
A.4:5
B.2:5
C.![]()
:2
D.![]()
: ![]()
参考答案:
【答案】A
【解析】解:如图1,连接OD,
∵四边形ABCD是正方形,
∴∠DCB=∠ABO=90°,AB=BC=CD=1,
∵∠AOB=45°,
∴OB=AB=1,
由勾股定理得:OD= ![]() =
= ![]() ,
,
∴扇形的面积是 ![]() =
= ![]() π;
π;
如图2,连接MB、MC,
∵四边形ABCD是⊙M的内接四边形,四边形ABCD是正方形,
∴∠BMC=90°,MB=MC,
∴∠MCB=∠MBC=45°,
∵BC=1,
∴MC=MB= ![]() ,
,
∴⊙M的面积是π×( ![]() )2=
)2= ![]() π,
π,
∴扇形和圆形纸板的面积比是 ![]() π÷(
π÷( ![]() π)=
π)= ![]() ,
,
即圆形纸片和扇形纸片的面积比是4:5.
故选A.
【考点精析】解答此题的关键在于理解扇形面积计算公式的相关知识,掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(﹣1,﹣
 ),点C的坐标为(2
),点C的坐标为(2  ,c),那么a,c的值分别是( )
,c),那么a,c的值分别是( ) 
A.a=﹣1,c=﹣
B.a=﹣2 ,c=﹣2
,c=﹣2
C.a=1,c=
D.a=2 ,c=2
,c=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过点(﹣1,0),康康依据图象写出了四个结论:
①如果点(﹣ ,y1)和(2,y2)都在抛物线上,那么y1<y2;
,y1)和(2,y2)都在抛物线上,那么y1<y2;
②b2﹣4ac>0;
③m(am+b)<a+b(m≠1的实数);
④ =﹣3.
=﹣3.
康康所写的四个结论中,正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△A1B1C1关于直线l对称,将△A1B1C1向右平移得到△A2B2C2,由此得出下列判断:①∠A=∠A2;②A1B1=A2B2;③AB∥A2B2.其中正确的是( )
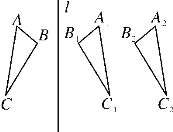
A. ①② B. ②③ C. ①③ D. ①②③
-
科目: 来源: 题型:
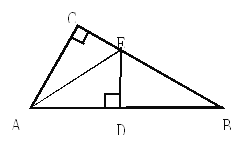
查看答案和解析>>【题目】如图所示,在△ABC中, ∠C=90°,DE为AB的垂直平分线,D为垂足,且EC=DE,则∠B 度数为__________
-
科目: 来源: 题型:
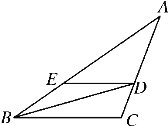
查看答案和解析>>【题目】如图,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠A=45°,∠BDC=60°.求△BDE各内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在正方形ABCD的边CD上,把△ADE绕点A顺时针旋转90°至△ABF位置,如果AB=
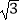 ,∠EAD=30°,那么点E与点F之间的距离等于 .
,∠EAD=30°,那么点E与点F之间的距离等于 . 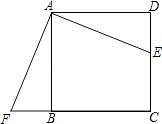
相关试题

