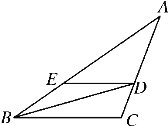
【题目】如图,△ABC与△A1B1C1关于直线l对称,将△A1B1C1向右平移得到△A2B2C2,由此得出下列判断:①∠A=∠A2;②A1B1=A2B2;③AB∥A2B2.其中正确的是( )
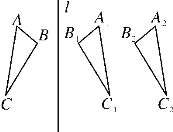
A. ①② B. ②③ C. ①③ D. ①②③
参考答案:
【答案】A
【解析】
根据图形对称的知识,可得△ABC≌△A1B1C1,结合图形平移的知识,知△A1B1C1≌△A2B2C2,A1B1∥A2B2,由△ABC≌△A1B1C1,△A1B1C1≌△A2B2C2得△ABC≌△A2B2C2,再结合全等三角形的性质,即可得到答案.
因为△ABC与△A1B1C1关于直线![]() 对称,
对称,
所以△ABC≌△A1B1C1.
因为△A1B1C1向右平移得到△A2B2C2,
所以△A1B1C1≌△A2B2C2,A1B1∥A2B2,但AB与A2B2不平行.
∵△ABC≌△A1B1C1,△A1B1C1≌△A2B2C2,
∴△ABC≌△A2B2C2,
∴∠CAB=∠C2A2B2,A1B1=A2B2.
综上可得,①和②是正确的.
故答案选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC=
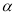 ,∠DCE=
,∠DCE= 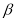 .
.① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究
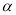 与
与 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时
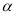 与
与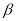 之间的数量关系(不需证明).
之间的数量关系(不需证明).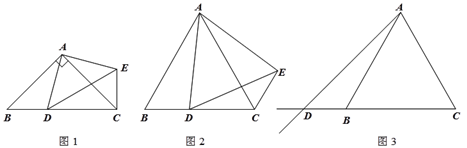
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(﹣1,﹣
 ),点C的坐标为(2
),点C的坐标为(2  ,c),那么a,c的值分别是( )
,c),那么a,c的值分别是( ) 
A.a=﹣1,c=﹣
B.a=﹣2 ,c=﹣2
,c=﹣2
C.a=1,c=
D.a=2 ,c=2
,c=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过点(﹣1,0),康康依据图象写出了四个结论:
①如果点(﹣ ,y1)和(2,y2)都在抛物线上,那么y1<y2;
,y1)和(2,y2)都在抛物线上,那么y1<y2;
②b2﹣4ac>0;
③m(am+b)<a+b(m≠1的实数);
④ =﹣3.
=﹣3.
康康所写的四个结论中,正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )

A.4:5
B.2:5
C.
:2
D.
:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中, ∠C=90°,DE为AB的垂直平分线,D为垂足,且EC=DE,则∠B 度数为__________
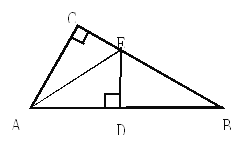
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠A=45°,∠BDC=60°.求△BDE各内角的度数.
相关试题

