【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1).下列结论:①2a+b>0;②abc<0; ③若OC=2OA,则2b﹣ac=4; ④3a﹣c<0.其中正确的个数是( ) 
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:①∵抛物线的开口向下, ∴a<0.
∵抛物线的对称轴﹣ ![]() >1,
>1,
∴b>﹣2a,即2a+b>0,①成立;
②∵b>﹣2a,a<0,
∴b>0,
∵抛物线与y轴的交点在y轴的负半轴,
∴c<0,
∴abc>0,②错误;
③点A的横坐标为 ![]() ,点C的纵坐标为c,
,点C的纵坐标为c,
∵OC=2OA,
∴﹣c= ![]() ,整理得:2b﹣ac=4,③成立;
,整理得:2b﹣ac=4,③成立;
④∵抛物线的对称轴1<﹣ ![]() <2,
<2,
∴﹣2a<b<﹣4a,
∵当x=1时,y=a+b+c>0,
∴a﹣4a+c>0,即3a﹣c<0,④正确.
综上可知正确的结论有3个.
故选C.
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.

(1)求E点坐标;
(2)设抛物线的解析式为y=a(x﹣h)2+k,求a,h,k;
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点M,N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形
 的边长为4,边
的边长为4,边 在
在 轴上,边
轴上,边 在
在 轴上,点
轴上,点 是
是 轴上一点,坐标为
轴上一点,坐标为 ,点
,点 为
为 的中点,连接
的中点,连接 .
.(1)点
 的坐标为;
的坐标为;(2)判断
 的形状,并证明你的结论.
的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于点E,∠E=30°,交AB于点D,连接AE,则SADC:S△ADE的比值为( )
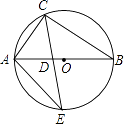
A.
B.
C.
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=x2的图象向右平移2个单位得函数y1的图象,将y与y1合起来构成新图象,直线y=m被新图象依次截得三段的长相等,则 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,且
,且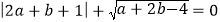 .
.(1)求
 的值;
的值;(2)①在
 轴的正半轴上存在一点
轴的正半轴上存在一点 ,使
,使 ,求点
,求点 的坐标;
的坐标;②在坐标轴上一共存在多少个点
 ,使
,使 成立?请直接写出符合条件的点
成立?请直接写出符合条件的点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,对于任意三点
中,对于任意三点 的“矩面积”,给出如下定义:“水平底”
的“矩面积”,给出如下定义:“水平底” 为任意两点横坐标差的最大值,“铅垂高”
为任意两点横坐标差的最大值,“铅垂高”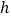 为任意两点纵坐标差的最大值,则“矩面积”
为任意两点纵坐标差的最大值,则“矩面积” .
.例如:三点坐标分别为
 ,则“水平底”
,则“水平底” ,“铅垂高”
,“铅垂高” ,“矩面积”
,“矩面积” .
.(1)已知点
 .
.①若
 三点的“矩面积”为12,求点
三点的“矩面积”为12,求点 的坐标;
的坐标;②求
 三点的“矩面积”的最小值.
三点的“矩面积”的最小值.(2)已知点
 ,其中
,其中 .若
.若 三点的“矩面积”为8,求
三点的“矩面积”为8,求 的取值范围.
的取值范围.
相关试题

