搜索
【题目】如图，在反比例函数y= 
（x＞0）的图象上，有点P1 ， P2 ， P3 ， P4…Pn（n为正整数，且n≥1）．它们的横坐标依次为1，2，3，4…n（n为正整数，且n≥1），分别过这些点作x轴与y轴的垂线，连接相邻两点，图中所构成的阴影部分的面积从左到右依次为S1 ， S2 ， S3…Sn﹣1（n为正整数，且n≥2），那么S2+S3+S4+…S7= ． 
参考答案：
【答案】
【解析】解：当x=1时，P1的纵坐标为4， 当x=2时，P2的纵坐标为2，
当x=3时，P3的纵坐标为 
，
当x=4时，P4的纵坐标为1，
当x=5时，P5的纵坐标为 
，
…
则S1= 
×1×（4﹣2）=1=2﹣1；
S2= ×1×（2﹣ ）= 
=1﹣ 
；
S3= ×1×（ ﹣1）= 
= ﹣ 
；
S4= ×1×（1﹣ ）= 
= ﹣ 
；
…
Sn= 
﹣ 
；
∴S2+S3+S4+…+S7
=1﹣ + ﹣ +…+ 
﹣ 
=1﹣ 
= ，
所以答案是： ．
【考点精析】关于本题考查的比例系数k的几何意义，需要了解几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知正方形ABCD，E为平面内任意一点，连结DE，将线段DE绕点D顺时针旋转90°得到DG，连结EC，AG．
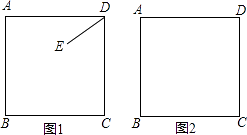
（1）当点E在正方形ABCD内部时，
①依题意补全图形；
②判断AG与CE的数量关系与位置关系并写出证明思路．
（2）当点B，D，G在一条直线时，若AD=4，DG=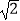
，求CE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】设在一个变化过程中有两个变量x与y，如果对于x的每一个值，y都有唯一确定的值和它对应，那么就说y是x的函数，记作y=f（x）．在函数y=f（x）中，当自变量x=a时，相应的函数值y可以表示为f（a）．
例如：函数f（x）=x2﹣2x﹣3，当x=4时，f（4）=42﹣2×4﹣3=5在平面直角坐标系xOy中，对于函数的零点给出如下定义：
如果函数y=f（x）在a≤x≤b的范围内对应的图象是一条连续不断的曲线，并且f（a）．f（b）＜0，那么函数y=f（x）在a≤x≤b的范围内有零点，即存在c（a≤c≤b），使f（c）=0，则c叫做这个函数的零点，c也是方程f（x）=0在a≤x≤b范围内的根．
例如：二次函数f（x）=x2﹣2x﹣3的图象如图1所示．
观察可知：f（﹣2）＞0，f（1）＜0，则f（﹣2）．f（1）＜0．所以函数f（x）=x2﹣2x﹣3在﹣2≤x≤1范围内有零点．由于f（﹣1）=0，所以，﹣1是f（x）=x2﹣2x﹣3的零点，﹣1也是方程x2﹣2x﹣3=0的根．
（1）观察函数y1=f（x）的图象2，回答下列问题：
①f（a）f（b） 0（“＜”“＞”或“=”）
②在a≤x≤b范围内y1=f（x）的零点的个数是 ．
（2）已知函数y2=f（x）=﹣
的零点为x1 ， x2 ， 且x1＜1＜x2 ．
①求零点为x1 ， x2（用a表示）；
②在平面直角坐标xOy中，在x轴上A，B两点表示的数是零点x1 ， x2 ， 点 P为线段AB上的一个动点（P点与A、B两点不重合），在x轴上方作等边△APM和等边△BPN，记线段MN的中点为Q，若a是整数，求抛物线y2的表达式并直接写出线段PQ长的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，线段AC和直线l分别垂直线段AB于点A，B．点P是线段AB上的一个动点，由A移动到B，连接CP，过点P作PD⊥CP交l于点D，设线段AP的长为x，BD的长为y，在下列图象中，能大致表示y与x之间函数关系的是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，D是AC上一点，联结BD，∠CBD=∠A．
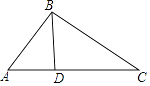
（1）求证：△CBD∽△CAB；
（2）若D是AC中点，CD=3，求BC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知反比例函数y=
的图象经过点P（﹣1，﹣1）．
（1）求此函数的表达式；
（2）画出此函数在第一象限内的图象．
（3）根据函数图象写出此函数的一条性质． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD∽四边形EFGH，连接相应的对角线AC，EG．
（1）求证△ABC∽△EFG；
（2）若
= 
，直接写出四边形ABCD与四边形EFGH的面积比为 ．
相关试题
