【题目】如图,二次函数y=a![]() +bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )

A. abc<0 B. 2a+b<0 C. a-b+c<0 D. 4ac-b2<0
参考答案:
【答案】D
【解析】试题分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:A、根据图示知,抛物线开口方向向上,则a>0.
抛物线的对称轴x=﹣![]() =1>0,则b<0.
=1>0,则b<0.
抛物线与y轴交与负半轴,则c<0,
所以abc>0.
故A选项错误;
B、∵x=﹣![]() =1,
=1,
∴b=﹣2a,
∴2a+b=0.
故B选项错误;
C、∵对称轴为直线x=1,图象经过(3,0),
∴该抛物线与x轴的另一交点的坐标是(﹣1,0),
∴当x=﹣1时,y=0,即a﹣b+c=0.
故C选项错误;
D、根据图示知,该抛物线与x轴有两个不同的交点,则△=b2﹣4ac>0,则4ac﹣b2<0.
故D选项正确;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】泰兴市为进一步改善生态环境决定对街道进行绿化建设,为此准备购进甲、乙两种树木、已知甲种树木的单价为
 元,乙种树木的单价为
元,乙种树木的单价为 元.
元.(1)若
 街道购买甲、乙两种树木共花费
街道购买甲、乙两种树木共花费 元,其中,乙种树木是甲种树木的一半多
元,其中,乙种树木是甲种树木的一半多 棵,请求出该街道购买的甲、乙两种树木各多少棵;
棵,请求出该街道购买的甲、乙两种树木各多少棵;(2)相关资料表明:甲种树木的成活率为
 ,乙种树木的成活率为
,乙种树木的成活率为 .现
.现 街道购买甲、乙两种树木共
街道购买甲、乙两种树木共 棵,为了使这批树木的总成活率不低于
棵,为了使这批树木的总成活率不低于 ,则甲种树木至多购买多少棵?
,则甲种树木至多购买多少棵? -
科目: 来源: 题型:
查看答案和解析>>【题目】对某一个函数给出如下定义:若存在实数
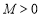 ,对于任意的函数值
,对于任意的函数值 ,都满足
,都满足 ,则称这个函数是有界函数,在所有满足条件的
,则称这个函数是有界函数,在所有满足条件的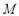 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
(1)分别判断函数

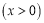 和
和 是不是有界函数?若是有界函数,求其边界值;
是不是有界函数?若是有界函数,求其边界值;(2)若函数
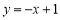
 的边界值是2,且这个函数的最大值也是2,求
的边界值是2,且这个函数的最大值也是2,求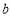 的取值范围;
的取值范围;(3)将函数
 的图象向下平移
的图象向下平移 个单位,得到的函数的边界值是
个单位,得到的函数的边界值是 ,当
,当 在什么范围时,满足
在什么范围时,满足 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
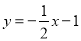 与
与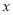 轴交于点A,与
轴交于点A,与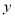 轴交于点B,抛物线
轴交于点B,抛物线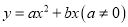 经过原点和点C(4,0),顶点D在直线AB上。
经过原点和点C(4,0),顶点D在直线AB上。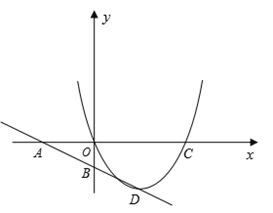
(1)求这个抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以P、C、D为顶点的三角形与△ACD相似。若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点Q是
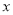 轴上方的抛物线上的一个动点,若
轴上方的抛物线上的一个动点,若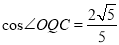 ,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1, 将Cl绕点B中心对称变换得C2, C2与x轴交于另一点C,将C2绕点C中心对称变换得C3, 连接C与C3的顶点,则图中阴影部分的面积为( )
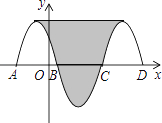
A. 32 B. 24 C. 36 D. 48
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=
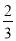 x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣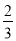 )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )
A. 大于0 B. 等于0 C. 小于0 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
相关试题

