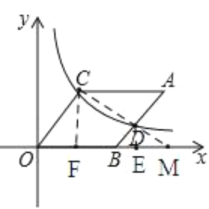
【题目】如图,在平面直角坐标系中,平行四边形ABOC的边OB在x轴上,过点C(3,4)的双曲线与AB交于点D,且AC=2AD,则点D的坐标为_____.

参考答案:
【答案】(7,![]() ).
).
【解析】
如图,作CF⊥OB于点F,作DE⊥OB于点E,连接CD并延长CD交x轴于点M,根据勾股定理求得OC=5,设AC=2a,则AD=a,OB=2a,DB=5-a,证明△COF∽△DBE,根据相似三角形的性质求得![]() ,
,![]() ,即可得D(
,即可得D(![]() ,
,![]() ),因为点D在反比例函数
),因为点D在反比例函数![]() 的图象上,可得方程
的图象上,可得方程![]() ·
·![]() =12,解得a=
=12,解得a=![]() 或a=0(舍去);从而求得点D的坐标.
或a=0(舍去);从而求得点D的坐标.
如图,作CF⊥OB于点F,作DE⊥OB于点E,连接CD并延长CD交x轴于点M,
设反比例函数的解析式为![]() ,把点C(3,4)代入求得k=12,即
,把点C(3,4)代入求得k=12,即![]() ;
;
∵四边形ABOC是平行四边形,
∴AC∥OB,OC∥AB,AC=OB,AB=OC,
∵C(3,4)
∴OF=3,CF=4,
在Rt△CFO中,根据勾股定理求得OC=5,
∴AB=5.
设AC=2a,则AD=a,OB=2a,
∴DB=5-a,
∵OC∥AB,
∴∠COF=∠DBE,
∵∠CFO=∠BED=90°,
∴△COF∽△DBE,023
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴OE=![]() ,
,
∴D(![]() ,
,![]() ),
),
∵点D在反比例函数![]() 的图象上,
的图象上,
∴![]() ·
·![]() =12,
=12,
解得a=![]() 或a=0(舍去);
或a=0(舍去);
∴D(7,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点
 ,
, 与坐标原点O在同一直线上,且AO=BO,其中m,n满足
与坐标原点O在同一直线上,且AO=BO,其中m,n满足 .
.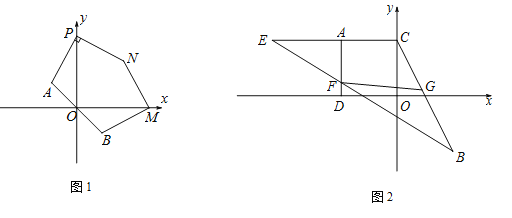
(1)求点A,B的坐标;
(2)如图1,若点M,P分别是x轴正半轴和y轴正半轴上的点,点P的纵坐标不等于2,点N在第一象限内,且
 ,PA⊥PN,
,PA⊥PN, ,求证:BM⊥MN;
,求证:BM⊥MN;(3)如图2,作AC⊥y轴于点C,AD⊥x轴于点D,在CA延长线上取一点E,使
 ,连结BE交AD于点F,恰好有
,连结BE交AD于点F,恰好有 ,点G是CB上一点,且
,点G是CB上一点,且 ,连结FG,求证:
,连结FG,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点为 A(2,2),B(5,3),C(3,5).

(1)请作出△ABC关于y轴的对称图形△A1B1C1,并写出点A的对称点A1的坐标;
(2)点M是第一象限内一点(不与点A重合),且M点的横、纵坐标都为整数.
①若
 ,请直接写出一个满足条件的M点的坐标;
,请直接写出一个满足条件的M点的坐标;②若
 ,请直接写出一个满足条件的M点的坐标;
,请直接写出一个满足条件的M点的坐标;(3)将△A1B1C1向右平移n个单位长度得到△A2B2C2,若△ABC与△A2B2C2关于某条直线l对称,则直线l与x轴交点的横坐标为 (用含n的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A.在△ABC中,若∠B=∠C﹣∠A,则△ABC是直角三角形
B.在△ABC中,若a
 =(b+c) (b﹣c),则△ABC是直角三角形
=(b+c) (b﹣c),则△ABC是直角三角形C.在△ABC中,若∠A:∠B:∠C=3:4:5,则△ABC是直角三角形
D.在△ABC中,若a:b:c=3:4:5,则△ABC是直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC,分别交AB、AC于点D、E,那么下列结论:①△BDF和△CEF都是等腰三角形;②F为DE中点;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的有( )

A.①③B.①②③C.①②D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P为△ABC三边垂直平分线的交点,∠PAC=20°,∠PCB=30°,

(1)求∠PAB的度数;
(2)直接写出∠APB与∠ACB的数量关系 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边落在坐标轴上,反比例函数y=
 的图象在第一象限的分支过AB的中点D交OB于点E,连接EC,若△OEC的面积为12,则k=_____.
的图象在第一象限的分支过AB的中点D交OB于点E,连接EC,若△OEC的面积为12,则k=_____.
相关试题

