【题目】如图,直线y=kx+b与x轴y轴分别交于点E、F,点E的坐标为(8,0),点F的坐标为(0,6),点A的坐标为(6,0).
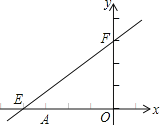
(1)求k和b的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,求出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() .
.
参考答案:
【答案】(1)![]() (2)S =
(2)S =![]() x+18(-8<x<0) (3)P点坐标为(-
x+18(-8<x<0) (3)P点坐标为(-![]() ,
,![]() )
)
【解析】
(1)用待定系数法直接求出;
(2)先求出OA,表示出PD,用三角形面积公式求解即可;
(3)利用(2)中得到的函数关系式直接代入S值,求出x即可.
(1)∵点E(-8,0),F(0,6)在直线y=kx+b上
∴![]() ,
,
解得![]()
(2)如图,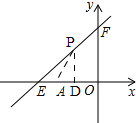
设点P的坐标为(x,y),并作PD⊥x轴于点D,
∵点P(x,y)在直线解析式为y=![]() x+6上,
x+6上,
∴PD=![]() x+6
x+6
∵点A的坐标为(-6,0)
∴OA=6,
∴S =![]() OAPD=
OAPD=![]() ×6(
×6(![]() x+6)=
x+6)=![]() x+18(-8<x<0),
x+18(-8<x<0),
(3)∵S△OPA=![]() x+18,
x+18,
当△OPA的面积为![]() 时,则
时,则![]() =
=![]() x+18,
x+18,
解得x=-![]() ,
,
∴P点坐标为(-![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米.如果梯子的顶端沿墙面下滑0.4米,那么点B将向左滑动多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(1)本次接受调查的跳水运动员人数为 ,图①中
 的值为 ;
的值为 ; (2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动,当点P运动到点B停止时,点Q也随之停止运动,问:
(1)P、Q两点从开始出发多长时间时,四边形PBCQ的面积是33
 ?
?(2)P、Q两点从开始出发多长时间时,点P与Q之间的距离是10cm?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列定理中,逆命题是假命题的是( )
A.等腰三角形的底角相等;
B.全等三角形的对应角相等;
C.直角三角形斜边上的中线等于斜边的一半;
D.线段垂直平分线上的任意一点到这条线段两个端点的距离相等。
-
科目: 来源: 题型:
查看答案和解析>>【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人同时从A地前往相距5千米的B地,甲骑自行车,途中修车耽误了20分钟,甲行驶的路程s(千米)关于时间t(分钟)的函数图像如图所示;乙慢跑所行的路程s(千米)关于时间t(分钟)的函数解析式为
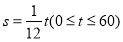
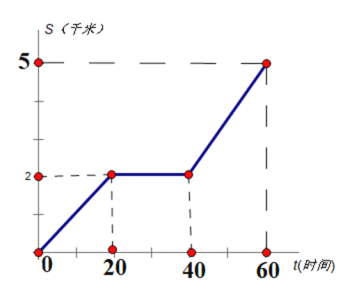
(1)在图中画出乙慢跑所行的路程关于时间的函数图像:
(2)甲修车后行驶的速度是每分钟_______米;
(3)甲、乙两人在出发后,中途_________分钟时相遇
相关试题

