【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

参考答案:
【答案】80或120
【解析】本题可以图形的旋转问题转化为点B绕D点逆时针旋转的问题,故可以D点为圆心,DB长为半径画弧,第一次与原三角形交于斜边AB上的一点B′,交直角边AC于B″,此时DB′=DB,DB″=DB=2CD,由等腰三角形的性质求旋转角∠BDB′的度数,在Rt△B″CD中,解直角三角形求∠CDB″,可得旋转角∠BDB″的度数.
解:如图,在线段AB取一点B′,使DB=DB′,在线段AC取一点B″,使DB=DB″,
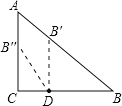
∴①旋转角m=∠BDB′=180°-∠DB′B-∠B=180°-2∠B=80°,
②在Rt△B″CD中,∵DB″=DB=2CD,∴∠CDB″=60°,
旋转角∠BDB″=180°-∠CDB″=120°.
故答案为:80°或120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动,当点P运动到点B停止时,点Q也随之停止运动,问:
(1)P、Q两点从开始出发多长时间时,四边形PBCQ的面积是33
 ?
?(2)P、Q两点从开始出发多长时间时,点P与Q之间的距离是10cm?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b与x轴y轴分别交于点E、F,点E的坐标为(8,0),点F的坐标为(0,6),点A的坐标为(6,0).
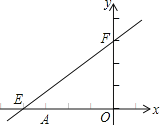
(1)求k和b的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,求出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当点P运动到什么位置时,△OPA的面积为
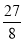 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列定理中,逆命题是假命题的是( )
A.等腰三角形的底角相等;
B.全等三角形的对应角相等;
C.直角三角形斜边上的中线等于斜边的一半;
D.线段垂直平分线上的任意一点到这条线段两个端点的距离相等。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人同时从A地前往相距5千米的B地,甲骑自行车,途中修车耽误了20分钟,甲行驶的路程s(千米)关于时间t(分钟)的函数图像如图所示;乙慢跑所行的路程s(千米)关于时间t(分钟)的函数解析式为
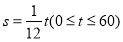
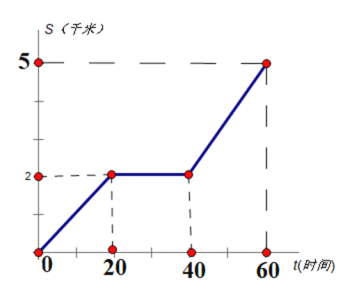
(1)在图中画出乙慢跑所行的路程关于时间的函数图像:
(2)甲修车后行驶的速度是每分钟_______米;
(3)甲、乙两人在出发后,中途_________分钟时相遇
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D为△ABC内一点, ∠BAD=15°,AD=AC,CE⊥AD于E,且CE=5.
(1)求BC的长;
(2)求证:BD=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知正比例函数图像经过点A(2,3)、B(m,6).
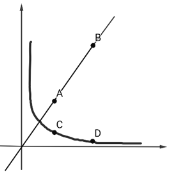
(1)求正比例函数的解析式.
(2)求m的值及A、B两点之间的距离。
(3)分别过点A与点B作y轴的平行线,与反比例函数在第一象限内的分支分别交于点C、D(点C、D均在点A、B下方),若BD=5AC.求反比例函数的解析式,并求出四边形ACDB的面积。
相关试题

