【题目】如图,抛物线![]() 过点
过点![]() ,
, ![]() .
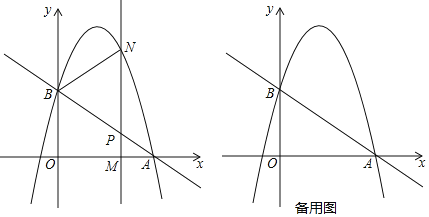
. ![]() 为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)如果以B,P,N为顶点的三角形与![]() 相似,求点M的坐标.
相似,求点M的坐标.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)N(
;(2)N(![]() ,
,![]() );(3)M(
);(3)M(![]() ,0)或M(
,0)或M(![]() ,0) .
,0) .
【解析】分析: (1)利用待定系数法求直线和抛物线解析式;
(2)先表示出N(m,- ![]() m2+
m2+![]() m+2),P(m,-
m+2),P(m,-![]() m+2),则计算出NP=-
m+2),则计算出NP=-![]() m2+4m,PM=-
m2+4m,PM=-![]() m+2,则利用NP=PM得到-
m+2,则利用NP=PM得到-![]() m2+4m=-
m2+4m=-![]() m+2,然后解方程求出m即可得到N点坐标;
m+2,然后解方程求出m即可得到N点坐标;
(3)利用两点间的距离公式计算出AB=![]() ,BP=
,BP=![]() m,NP=-
m,NP=-![]() m2+4m,由于∠BPN=∠ABO,利用相似三角形的判定方法,当
m2+4m,由于∠BPN=∠ABO,利用相似三角形的判定方法,当![]() 时,△BPN∽△OBA,则△BPN∽△MPA,即
时,△BPN∽△OBA,则△BPN∽△MPA,即 ;当
;当![]() 时,△BPN∽△ABO,则△BPN∽△APM,即
时,△BPN∽△ABO,则△BPN∽△APM,即 ,然后分别解关于m的方程即可得到对应的M点的坐标.
,然后分别解关于m的方程即可得到对应的M点的坐标.
详解:
(1)解:设直线![]() 的解析式为
的解析式为![]() (
(![]() )
)
∵![]() ,
, ![]()
∴![]() 解得
解得
∴直线![]() 的解析式为
的解析式为![]()
∵抛物线![]() 经过点
经过点![]() ,
, ![]()
∴ 解得
解得
∴![]()
(2)∵![]() 轴,
轴, ![]() 设
设![]() ,
, ![]()
∴![]() ,
, ![]()
∵![]() 点是
点是![]() 的中点
的中点
∴![]()
∴![]()
解得![]() ,
, ![]() (不合题意,舍去)
(不合题意,舍去)
∴![]()
(3)∵![]() ,
, ![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]()
∵![]()
∴当![]() 与
与![]() 相似时,存在以下两种情况:
相似时,存在以下两种情况:
![]()
∴ 解得
解得![]()
∴![]()
![]()
∴ ,解得
,解得![]()
∴![]()
点睛: 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和相似三角形的判定与性质;会利用待定系数法求函数解析式;灵活应用相似比表示线段之间的关系;理解坐标与图形的性质;会利用分类讨论的思想解决数学问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程:(m﹣1)x2+(m﹣2)x﹣1=0(m为实数).
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)若
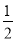 是此方程的实数根,抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积.
是此方程的实数根,抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积. -
科目: 来源: 题型:
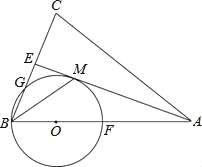
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,点
 、
、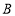 、
、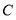 是三个格点(网格线的交点叫做格点)
是三个格点(网格线的交点叫做格点)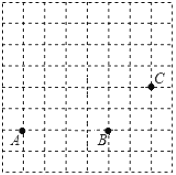
(1)画线段
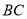 ,画射线
,画射线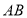 ,过点
,过点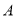 画
画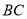 的平行线
的平行线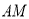 ;
;(2)过点
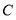 画直线
画直线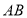 的垂线,垂足为点
的垂线,垂足为点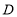 ,则点
,则点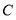 到
到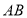 的距离是线段______的长度;
的距离是线段______的长度;(3)线段
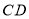 ______线段
______线段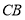 (填“>”或“<”),理由是______.
(填“>”或“<”),理由是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求
 的值.
的值. -
科目: 来源: 题型:
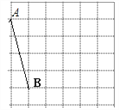
查看答案和解析>>【题目】如图网格中每个小正方形的边长均为1,线段AB、CD的端点都在小正方形的顶点上.
(1)图(1)中,画一个以线段AB一边的四边形ABEF,且四边形ABEF是面积为7的中心对称图形,点E、F都在小正方形的顶点上,并直接写出线段BE的长;
(2)在图(2)中,画一个以线段CD为斜边直角三角形CDG,且△CDG的面积是2,点G在小方形的顶点上。

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图像如图所示.根据图像提供的信息,解答下列问题:
(1)求营销员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式;
(2)若两个月内该营销员的销售量从2万件猛增到5万件,月收入两个月大幅度增长,且连续两个月的月收入的增长率是相同的,试求这个增长率(
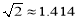 ,保留到百分位).
,保留到百分位).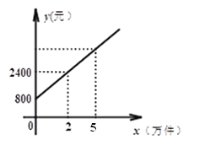
相关试题

