【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于M、N两点.
的图象交于M、N两点.
(1)根据图中条件求出反比例函数和一次函数的解析式;
(2)连结OM、ON,求△MON的面积;
(3)根据图象,直接写出使一次函数的值大于反比例函数的值的x的取值范围.

参考答案:
【答案】(1)y=2x﹣4.(2)8,(3)﹣1<x<0或x>3
【解析】
(1)把M(3,2)代入y=![]() ,即可求得m,得到y=
,即可求得m,得到y=![]() ,代入N(﹣1,a)求得a,得到N(﹣1,﹣6),把两点代入y=kx+b,解之即可求得k、b,从而求出两函数的解析式;
,代入N(﹣1,a)求得a,得到N(﹣1,﹣6),把两点代入y=kx+b,解之即可求得k、b,从而求出两函数的解析式;
(2)设直线MN交x轴于点A,求得A点坐标,然后根据S△MON=S△MOA+S△NOA求得即可;
(3)根据M,N的坐标即可得到结论.
解:(1)∵一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于M(3,2)、N(﹣1,a)两点
的图象交于M(3,2)、N(﹣1,a)两点
∴m=6,a=﹣6,
∴反比例函数y=![]() ,N(﹣1,﹣6),
,N(﹣1,﹣6),
把M(3,2),N(﹣1,﹣6)代入y=kx+b得![]() ,
,
解得![]() ,
,
∴一次函数的解析式的解析式为y=2x﹣4.
(2)设直线MN交x轴于点A,
当y=0时,2x﹣4=0,
∴x=2,
∴A(2,0),
∴S△MON=S△MOA+S△NOA=![]() OA(yM﹣yN)=
OA(yM﹣yN)=![]() ×2×8=8;
×2×8=8;
(3)由图象可知,当﹣1<x<0或x>3时一次函数的值大于反比例函数的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 边的垂直平分线
边的垂直平分线 交
交 于点
于点 ,
, 边的垂直平分线
边的垂直平分线 交
交 于点
于点 ,
, 与
与 相交于点
相交于点 ,联结
,联结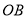 、
、 ,若
,若 的周长为
的周长为 ,
,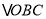 的周长为
的周长为 .
.
(1)求线段
 的长;
的长;(2)联结
 ,求线段
,求线段 的长;
的长;(3)若
 ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人沿相同的路线由
 到
到 匀速行进,
匀速行进, 两地间的路程为
两地间的路程为 他们行进的路程
他们行进的路程 与甲出发后的时间
与甲出发后的时间 之间的函数图像如图所示.根据图像信息,下列说法正确的是( )
之间的函数图像如图所示.根据图像信息,下列说法正确的是( )
A.甲的速度是
 B.乙的速度是
B.乙的速度是
C.乙比甲晚出发
 D.甲比乙晚到
D.甲比乙晚到 地
地
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,在下面五个结论中:
①2a﹣b=0;②c=﹣3a;③当m≠1时,a+b<am2+bm;
④若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2;
⑤使△ACB为等腰三角形的a值可以有三个.其中正确的结论是_________.(只填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是
 .
.(1)求暗箱中红球的个数;
(2)先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树形图或列表法求解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张准备把一根长为32cm的铁丝剪成两段,并把每一段各围成一个正方形.(1)要使这两个正方形的面积之和等于40cm2,小张该怎么剪?
(2)小李对小张说:“这两个正方形的面积之和不可能等于30cm2.”他的说法对吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

相关试题

