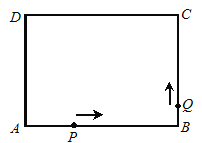
【题目】如图,矩形ABCD中,AB=4,BC=3,点P、Q分别从A、B两点出发,按逆时针方向沿矩形的边运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,运动的时间为t秒,当其中某一点到达点A时,运动停止,运动过程中,点P关于直线AQ的对称点记为点M.
(1)点P点在线段AB上运动,点Q在线段BC上运动时,请用含t的式子表示出△APQ的面积S;
(2)当点P在线段BC上运动,且△ABP∽△PCQ时,求t的值;
(3)若点Q在线段CD上,且以A、P、Q、M为顶点的四边形是菱形,求t的值.
参考答案:
【答案】(1)S=t2 (2)![]() (3)当t=1+
(3)当t=1+![]() 时,以A、P、Q、M为顶点的四边形是菱形
时,以A、P、Q、M为顶点的四边形是菱形
【解析】试题分析:(1)底AP=2t,高BQ=t,根据三角形性的的面积公式求解即可;
(2)根据相似三角形的性质列方程求解;
(3)分四种情况,①点P在BC上,点Q在CD上,此时不合题意;②点P和点Q都在CD上,P在Q的左边,此时不合题意;③点P和点Q都在CD上,P在Q的又边,根据勾股定理列方程求解;④点P在AD上,点Q在CD上,根据勾股定理列方程求解.
解:(1)AP=2t,BQ=t,∴S=t2.
(2)如图1,由△ABP∽△PCQ可知,此时点Q在线段CD上,∴![]() ,
,
即![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∵![]() ,∴
,∴![]() .
.
(3)①当3<t≤![]() 时,如图2,以A、P、Q、M为顶点的四边形不可能是菱形;
时,如图2,以A、P、Q、M为顶点的四边形不可能是菱形;
②当![]() <t≤4时,如图3,以A、P、Q、M为顶点的四边形不可能是菱形;
<t≤4时,如图3,以A、P、Q、M为顶点的四边形不可能是菱形;
③当4<t≤![]() 时,如图4,若PA=PQ,则以A、P、Q、M为顶点的四边形是菱形,即32+(11-2t)2=(2t-t-4)2,整理得t2-12t+38=0,方程无解;
时,如图4,若PA=PQ,则以A、P、Q、M为顶点的四边形是菱形,即32+(11-2t)2=(2t-t-4)2,整理得t2-12t+38=0,方程无解;
④当![]() <t≤7时,如图5,若PA=PQ,则以A、P、Q、M为顶点的四边形是菱形,即(2t-11)2+(7-t)2=(14-2t)2,解得t=1±
<t≤7时,如图5,若PA=PQ,则以A、P、Q、M为顶点的四边形是菱形,即(2t-11)2+(7-t)2=(14-2t)2,解得t=1±![]() ,
,
∵![]() <t≤7,∴t=1+
<t≤7,∴t=1+![]() .
.
∴当t=1+![]() 时,以A、P、Q、M为顶点的四边形是菱形.
时,以A、P、Q、M为顶点的四边形是菱形.


-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有除颜色外都相同的红球和黄球,两种颜色的球一共有10个,每次摸出其中一个球,记下颜色后,放回搅匀.一个同学进行了反复试验,下面是做该试验获得的数据.
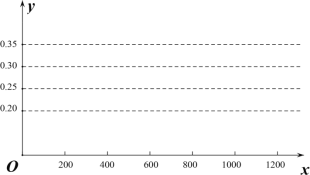
(1)a= ,画出摸到红球的频率的折线统计图;
(2)从这个袋子中任意摸一个球,摸到黄球的概率估计值是多少?(精确到0.1)
(3)怎样改变袋中红球或黄球的个数,可以使得任意摸一次,摸到两种颜色球的概率相等?(写出一种方案即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个函数y与自变量x的部分对应值如下表:

(1)从我们已学过的函数判断:y是x的 函数,y与x的函数关系式为 ;
(2)根据函数图像,当-2 x -
 时,求y的取值范围.
时,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,点D、E分别是边AB、AC上的两点(点D不与点A、 点B重合),且DE∥BC,以DE为一边,在四边形DBCE的内部作正方形DEFG,已知AB=AC=5,BC=6.
(1)试求△ABC的面积;
(2)当GF与BC重合时,求正方形DEFG的边长;
(3)若BG的长度等于正方形DEFG的边长,试求AD的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c﹣b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )
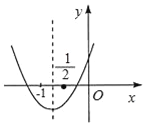
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把抛物线y=
 x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为________.
x2交于点Q,则图中阴影部分的面积为________. 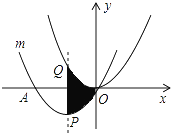
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划拨款9万元从厂家购进50台电视机,已知该厂生产三种不同型号的电视机,出厂价分别为甲种每台1500元, 乙种每台2100元, 丙种每台2500元, 若商场同时购进其中两种不同型号的电视机共50台,用去9万元.请你通过计算,说明商场有哪些进货方案.
相关试题

