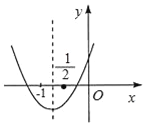
【题目】二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c﹣b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】由图象可知,a>0,b>0,c>0,
∵﹣![]()
![]() >﹣1,
>﹣1,
∴b<2a,故①正确,
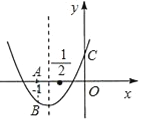
如图易知A(﹣1,0),B(﹣1,a﹣b+c),C(0,c),
当AB=OC时,﹣(a﹣b+c)=c,可得a+2c﹣b=0,
当AB>OC时,﹣(a﹣b+c)>c,可得a+2c﹣b<0,
当AB<OC时,﹣(a﹣b+c)<c,可得a+2c﹣b>0,
故②错误,
∵﹣![]()
![]() <﹣
<﹣![]()
![]() ,
,
∴b>a,
设x1>x2
∵﹣![]()
![]() <x1<0,﹣2<x2<﹣1,
<x1<0,﹣2<x2<﹣1,
∴x1x2<1,
∴![]()
![]() <1,
<1,
∴a>c,
∴b>a>c,故③正确,
∵b2﹣4ac>0,
∴2ac<![]()
![]() b2,
b2,
∵b<2a,
∴![]()
![]() <3ab,
<3ab,
∴![]()
![]() b2=b2+
b2=b2+![]()
![]() b2>b2+2ac,
b2>b2+2ac,
b2+2ac<![]()
![]() b2<3ab,
b2<3ab,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个函数y与自变量x的部分对应值如下表:

(1)从我们已学过的函数判断:y是x的 函数,y与x的函数关系式为 ;
(2)根据函数图像,当-2 x -
 时,求y的取值范围.
时,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,点D、E分别是边AB、AC上的两点(点D不与点A、 点B重合),且DE∥BC,以DE为一边,在四边形DBCE的内部作正方形DEFG,已知AB=AC=5,BC=6.
(1)试求△ABC的面积;
(2)当GF与BC重合时,求正方形DEFG的边长;
(3)若BG的长度等于正方形DEFG的边长,试求AD的长.


-
科目: 来源: 题型:
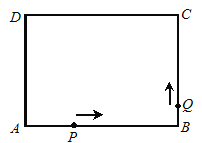
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=3,点P、Q分别从A、B两点出发,按逆时针方向沿矩形的边运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,运动的时间为t秒,当其中某一点到达点A时,运动停止,运动过程中,点P关于直线AQ的对称点记为点M.
(1)点P点在线段AB上运动,点Q在线段BC上运动时,请用含t的式子表示出△APQ的面积S;
(2)当点P在线段BC上运动,且△ABP∽△PCQ时,求t的值;
(3)若点Q在线段CD上,且以A、P、Q、M为顶点的四边形是菱形,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把抛物线y=
 x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为________.
x2交于点Q,则图中阴影部分的面积为________. 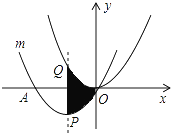
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划拨款9万元从厂家购进50台电视机,已知该厂生产三种不同型号的电视机,出厂价分别为甲种每台1500元, 乙种每台2100元, 丙种每台2500元, 若商场同时购进其中两种不同型号的电视机共50台,用去9万元.请你通过计算,说明商场有哪些进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△BAC中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
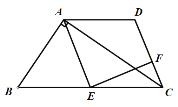
(1)求证:DC=EC.
(2)若AB=6,BC=10,求EF的长.
相关试题

